[Deep Learning] GCN - Graph Convolution Network

1. Intro

이전에 GNN 에 대하여 글을 작성을 하였었지만 이번에는 GNN 을 이용한 가장 대표적인 모델인 GCN 에 대하여 이야기를 해보겠습니다. GCN - Graph Convolution Network는 이름에서 처럼 Graph 에 대한 데이터를 convolution 작업을 통해서 데이터를 모델에 전달하는 방식입니다.

2. Related Work

2.1 Graph

출처 : https://github.com/heartcored98/Standalone-DeepLearning/blob/master/Lec9/Lec9-A.pdf

이전에도 이야기를 했지만 그래프 데이터의 구조는 기본적으로 노드(node) 와 간선(edge)들로 이루어져 있다. 그리고 이 노드들 간의 관계를 나타내는 방식이 Adjacency matrix(입접행렬)로 표현하면 노드가 간선으로 연결되어 있다면 1 아니면 0 으로 표시가 된다. 그리고 추가적으로 노드들의 정보 즉 데이터에 대한 부분은 Feature matrix로 노드들의 정보가 담긴 행렬도 그래프 데이터 구조를 설명한는데 필요로 한다.

2.2 Convolution Layer

출처 : https://learnopencv.com/understanding-convolutional-neural-networks-cnn/

convolution 에 대한 작업에 대하여 간단하게 이야기를 하자면 기존의 이미지에서 filter 를 이미지에서 사진과 같이 stride 의 범위 만큼 이동하면서 곱을 진행하고 이것을 output feature map의 한개의 output으로 변환을 한다. 이때 output feature map의 사이즈는 filter의 크기와 padding( 이미지 224*224 이외의 값을 이미지에 추가하여 input image 의 사이즈를 늘린다)으로 조절을 한다.

 

3. Proposed Method

3.1 Graph convolution

출처 : https://github.com/heartcored98/Standalone-DeepLearning/blob/master/Lec9/Lec9-A.pdf

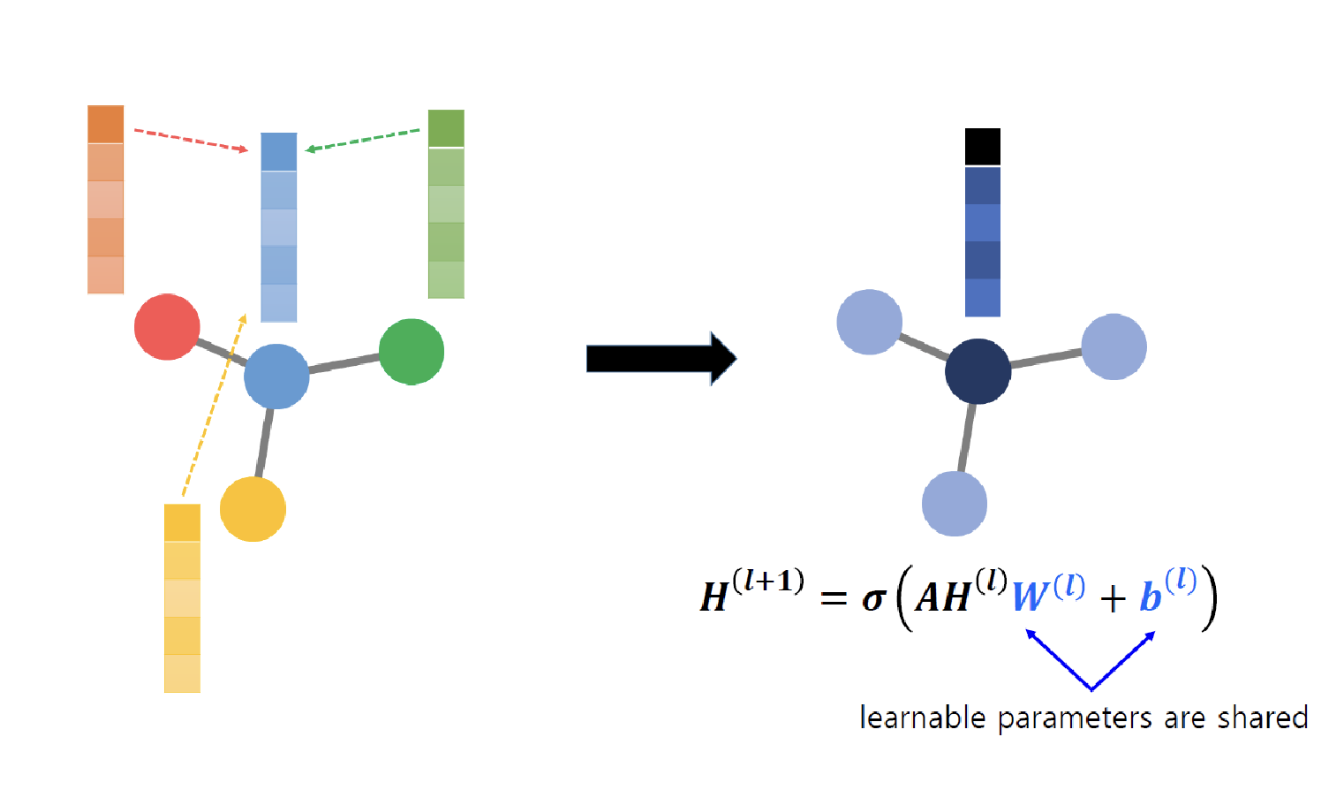
여기서 식은 간단하게 알아보면 $$ /sigma. 함수는 CNN 에서 convolution 연산 이후의 activation 함수를 이야기 한다.

그리고 H는 먼저 l 은 l 번째의 자신의 값을 표시하면 W는 l 번째의 Weight(filter 라고 생각해도 가능), b는 bias를 의미한다. 그렇게 수식을 말로 풀어서 설명하면 자기 현재 단계의 이전까지의 자신의 값과 그리고 관련된 근처의 노드들의 값을 각각 weight와 곱 연산을 진행하고 이것의 총 합을 activation 함수를 통해서 다음 단계의 값으로 업데이트 해주는 작업이다. 이것을 CNN 에서 convolution 작업을 진행하면서 이전 feature 에서 filter의 곱을 통해서 다음의 feature map을 생성하는 방식과 같다.

 

오른쪽 그림에서는 이런 연산을 모든 노드를 통해서 하는게 아니라 행렬의 곱으로 표현하는 방식을 설명한 수식이다. 이것을 연산 처리 속도를 더욱 빠르게 하기위한 작업이다. 

 

 

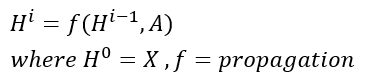
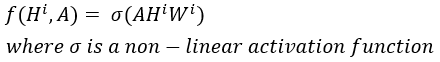
먼저 수식을 본다면 H^i 는 이전까지의 연산을 통해서 얻은 i 단계의 feature를 말합니다. (왼쪽)

오른쪽 그림은 f함수 연산에 대한 설명인데 AH^iW^i 를 모두 곱하는 방식이다. 이것은 아래 이미지로 더 자세하게 설명하겠다.

출처 : https://littlefoxdiary.tistory.com/17

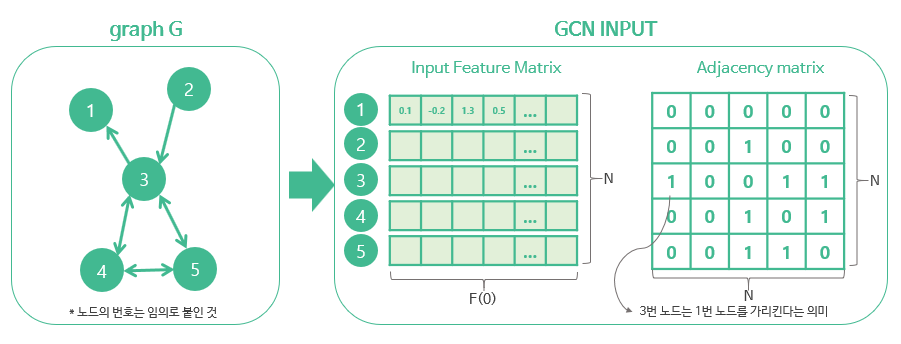
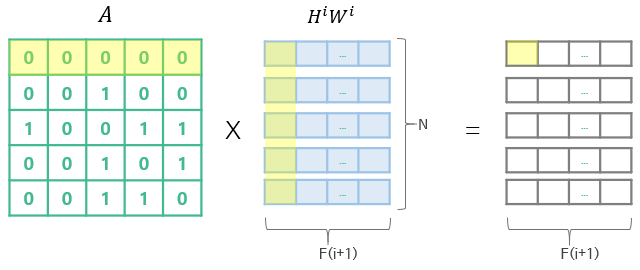
연산 f 에 대한 설명은 그림으로 더 설명을 해보자면 먼저 연산의 input 은 왼쪽 그림에서 처럼 노드들의 feature 와 Adjacency matrix 를 input 으로 받는다 f(H^i,A) 그리고 오른쪽 그림을 보면 feature 정보를 W와 곱 연산을 하는데 이것은 노드들의 feature를 Weight 와 곱을 해주는 작업입니다. 이것은 기존 CNN 방식처럼 필터를 곱하는 것과 같고 N* x의 차원으로 표시가 되며 N 은 노드의 수를 의미하지만 x 의 필터의 갯수 임으로 필터의 수로 지정이 된다. 그렇게 된다면 결과(H^i * W^i)는 N * x 차원의 feature matrix가 생성이 될것이고 이것을 다시 Adjacency matrix를 곱하게 된다면 각 연산을 처리한 노드들이 연관된 노드들의 정보만들 추출여 output feature matrix로 만들어주는 작업을 진행하게 된다.

 

  정리하자면 Graph 에서의 convolution작업은 feature matrix 를 filter weight matrix와 곱 연산을 진행하고 Adjacency matrix 와도 최종적으로 곱 연산을 진행하면 새로 생성된 feature matrix는 N * x 차원의 matrix가 되면서 convolution작업을 행렬의 곱으로 간단하게 연산이 가능하다. 

 

이렇게 된다면 기존의 CNN layer 와 같이 이미지에서 필터를 통해서 특징을 추출하는 convolution 방식처럼 graph 에서도 같은 방식으로 필터를 통해서 노드간의 관계의 특징을 추출하는 방식을 적용하는게 가능해진다. 

 

3.2 Readout - purmuation invariance

출처 : https://github.com/heartcored98/Standalone-DeepLearning/blob/master/Lec9/Lec9-A.pdf

 

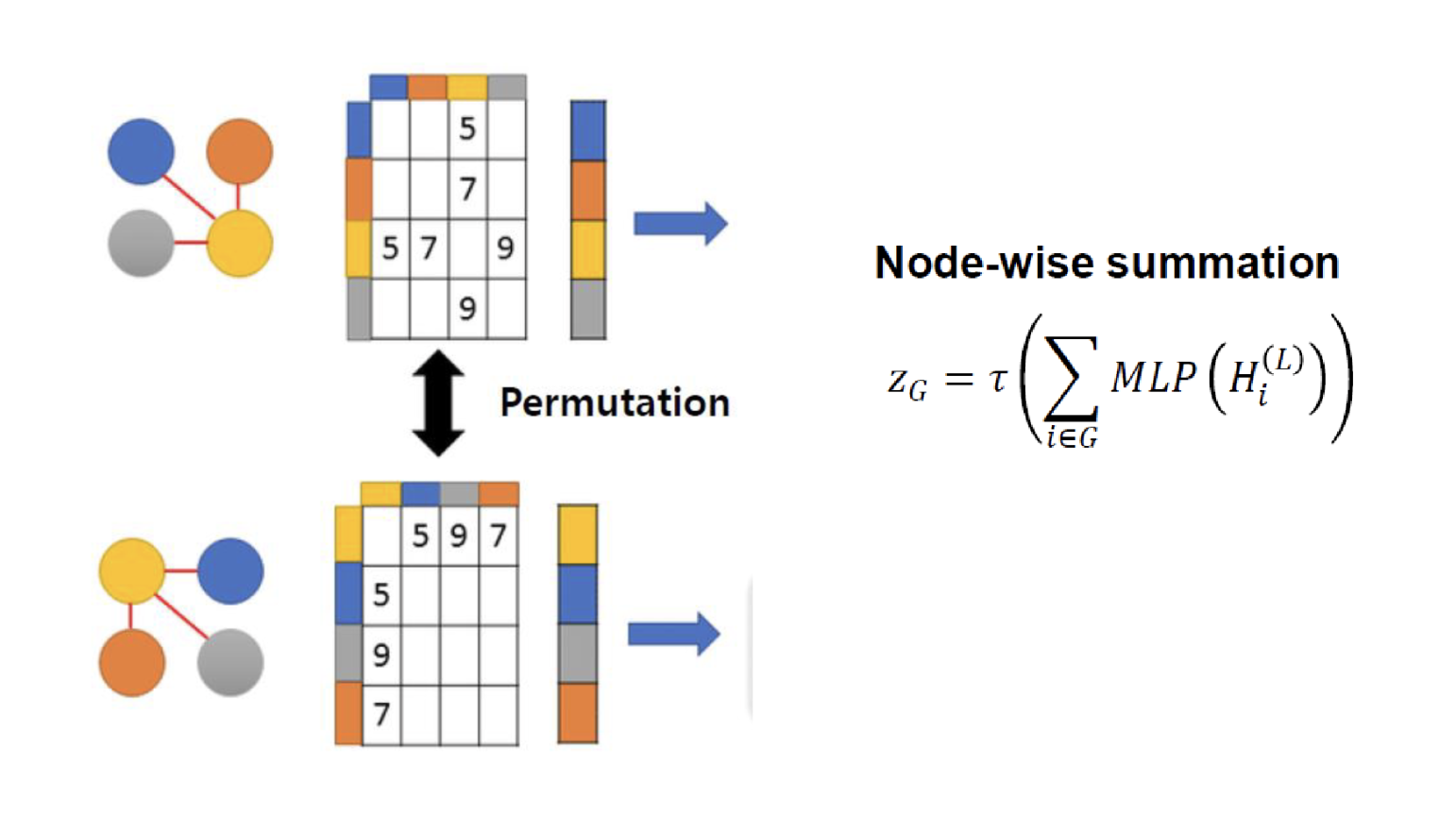
그래프에서 문제가 하나 있는데 그래프의 데이터는 같은 데이터라고 하더라고 Adjacency matrix 의 구조가 바뀌게 되면서 그렇다면 표현되는 node feature matrix 또한 바뀌게 된다. 이것을 해결하기 위해서는 Readout이라는 방식을 추가했다.