운동하는 공대생
[Deep Learning]Quantization (양자화) 본문
양자화에 대한 개념은 LLM 모델의 크기가 커짐에 따라서 당연하게 크기를 줄이는 방향으로 연구가 진행되면서 최근에 기본적으로 사용되는 이론이다.
양자화에 대한 개념을 말하기 전에 데이터에 대한 표현 방식을 먼저 이야기를 해보자면
integer는
3 → 11
12 → 1100
4bit integer
3 → 0011
12 → 1100
데이터에 대한 표현은 0과 1로 이루어져 있기 때문에 비트에 대한 제한을 준다면 4비트 int 같은 경우에는 0에서 15까지의 표현이 가능하다.
실제 우리가 사용되는 숫자의 표현은 int만이 사용되지 않고 실수를 많이 사용한다.
그렇다는 건 이것을 표현하기 위해서는 float 표현을 통해서 우리가 아는 실수를 모두 컴퓨터에서 표시를 한다.

float는 32, 16,8 등으로 표현이 가능하다. 그리고 이것은 실수를 표현하기 위해서 sign, exponent, fraction 부분으로 나뉘며 이는 수를 컴퓨터에서 표현하는 가장 기본적인 방식이다.
Rate & Distortion
예시를 통해 설명을 해보자면
ex) Heights ⇒154, 171, 163, 177, 181, 169, 171
2bit
150 ≤ x < 160 ⇒ 0 = 00
160 ≤ x < 170 ⇒ 1 = 01
170 ≤ x < 180 ⇒ 2 = 10
180 ≤ x < 190 ⇒ 3 = 11
이런 식으로 2bit로 표현이 가능하다.
다시 예를 들어 양자화가 된 2bit의 데이터가 있다고 한다면
001001 → 155,175,165 이렇게 양자화가 된 데이터를 원래의 데이터로 표현을 한다면 범위를 나타내는 구역의 중간 값을 복원한다.
하지만 여기서의 문제는 원래 가지고 있었던 값은 154 임으로 155로 복원하면 1 정도의 오차 범위가 생기게 된다.
cell : [150, 160)
value : 155
distortion = (154 - 155)^2
로 표현이 되며 이 방식은 error의 오차범위가 +- 5 정도이다.
3bit
[150, 155) ⇒ 000
[155, 160) ⇒ 001
이렇게 3비트로 표현을 한다면 오차 범위는 +- 2.5 정도이다.
2 bits more specific for data
이 방식은 데이터를 기반으로 구간을 설정하는 방식이다. 처음에 예시를 보였던 부분을 데이터를 기반으로 구역을 설정한다.
[154, 161) ⇒ 00
[161, 168) ⇒ 01
[168, 175) ⇒ 10
[175, 182) ⇒ 11
이렇게 한다면 error의 오차범위는 3.5 정도이다.
이런 형식으로 error 측면에서 범위를 설정을 잘한다면 즉 구역을 나누는걸 데이터를 기반으로 작게 가능하다면 max, min 값을 활용한다면 오차범위를 줄이는 방식이 가능해짐을 알 수 있다.
그래서 이 방식을 기반으로 Uniform 방식의 양자화 방식이 출발한다.
Uniform Quantization
이 방식을 적용하기 위해서는 몇 가지 사용되는 값들이 존재한다.
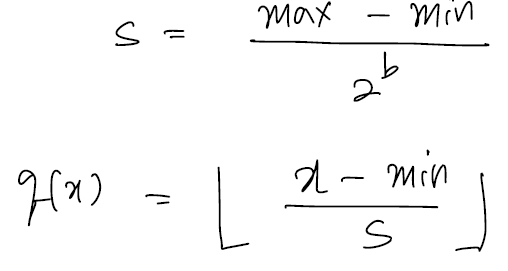
scale factor를 나타내는 s 값과 이 값을 사용해서 데이터를 양자화하는 방식이 q(x)이다.
이것을 많이 사용되는 min, max 양자화 방식을 이야기하며 uniform 방식이다.
간단하게 표현을 해보자면 가장 큰 값이랑 작은 값의 차이를 표현하고자 하는 cell의 개수로 나눠서 정의하는 방식이다.
What if outlier
outlier는 데이터의 이상치를 이야기하며 데이터가 몇 개만 너무 크거나 작은 몇 가지를 outlier라고 이야기를 한다. 하지만 이런 outlier의 문제는 양자화에서 항상 문제가 되는 부분이며 범위를 나누는 uniform quantization 범위의 구간을 크게 만드는 문제가 있어서 outlier를 처리해야 한다.
CLAMP
이 방식은 outlier를 처리하는 방식으로 일정 구간에 대하여 정의를 한다면 가령 그 범위를 벗어나는 큰 값이나 작은 값을 그 범위의 가장 큰 값 혹은 작은값으로 매핑하는 방식이다.
아까의 예시를 통해 설명을 하자면 182 보다 큰값 200이라는 값이 있다면 이 값을 182로 매핑해서 변환하는 방식이다.
이 방식은 200이라는 값만 본다고 한다면 error 값이 크지만 전체적으로 본다면 범위의 정확성이 올라가서 mean error 값이 작아지는 효과가 있다.
Non-uniform Quantization
기존 Uniform 방식에서 cell의 범위가 항상 일정하다는 문제를 해결하는 것이다.

non-uniform 방식은 기존의 uniform 방식과는 다르게 각각의 구간을 분포에 따라서 설정하는 방식이다.
분포를 나타내고 각각의 treshold를 정해서 데이터가 그 구역에 있다면 표현하고자 하는 비트의 값으로 표현하는 방식이다.
예를 들어 b가 4 일 때 즉 구간이 총 16개라 가정한다면 위에 있는 그림에서 a0 ~ a1의 구간에 들어가는 데이터는 모두 0000으로 양자화가 될 것이다.
이런 방식으로 양자화가 진행되는데 구역을 나누거나 최적화를 하는 방식은 아래에 설명을 해보겠다.
How to define parameters of Non-uniform method
위와 같은 조건일 때

q(x) = i
dec(i) = m
양자화를 하고 다시 원상 복구하는걸 m이라고 한다면 m은 각 구간별로 decoding 할 때 대치되는 값이다. (uniform에서는 중간값) 그리고 최적화를 해야 하는 objective function 은 아래와 같다.
그렇다면 최적화를 해야하는 부분을 알고 있다면 이런 구간에 대한 조건 즉 a 들의 구간을 설정하는 방식도 동반이 되어야 한다.
Lloyd Max
- Initialize a0, a1, …… a_2^b
- find m1, m2, ….. m_2^b
- update a0, a1 ….. a_2^b
a는 구간을 나누는 treshold 역할을 하는데 이것을 m의 값을 기준으로 update 시킨다.

m에 대한 추가 설명을 하자면 위에서도 설명했지만 구간에 대한 평균값을 사용한다 즉 중간을 사용하지 않는 건 분포이기 때문에 조금 더 정확한 값으로 대치하기 위해서이다.

→ 이제 2 & 3을 반복적으로 수행한다. 즉 구간을 나누는 3번과 다시 그 구간 내부에서의 m 값을 다시 구하면서 반복적으로 수행한다.
distortion 이 감소할 때까지 반복하며 이것은 언젠가 converge 한다.
2 m update → distortion down
3 a update → distortion down
'Deep Learning' 카테고리의 다른 글
| 삼성 갤럭시 S25 root (S25 root, SM-S931N) (0) | 2025.03.19 |
|---|---|
| 갤럭시 S25 에서 LLM 구동하기 (llama.cpp, Termux) (1) | 2025.03.12 |
| [Deep Learning] GCN - Graph Convolution Network (0) | 2023.07.04 |
| [Deep Learning] CNN-Convolutional Neural Networks (1) | 2023.04.27 |
| [Deep Learning] 다층 퍼셉트론 이론과 역전파 (0) | 2022.12.15 |




