운동하는 공대생
[Machine Learning] 머신러닝에서 딥러닝까지 이론 정리 (5) - Perceptron, Backpropagation 본문
[Machine Learning] 머신러닝에서 딥러닝까지 이론 정리 (5) - Perceptron, Backpropagation
운동하는 공대생 2024. 4. 8. 13:201. Intro
이제는 머신러닝에서 넘어와서 딥러닝에 대하여 정리를 해보겠다.
딥러닝 분야에서의 기본이 되는 개념은 뉴런이다.

뉴런은 사람의 뇌에 존재하는 뉴런을 모방한 기술로서 전기적인 신호를 가지고 뉴런끼리의 정보 전달의 역할을 모방했다. 그래서 Artificial neurons은 input을 받아들이고 output에서는 다음 뉴런으로 그 신호를 보낼지 말지를 결정한다.
이런 뉴런들을 모아서 모델을 구성한것을 Perceptron이라고 칭하며 Perceptron 여러 Layer를 구성하게 되고 다양한 방식으로 변형되면서 지금의 딥러닝의 모델들이 탄생했다.
2. Perceptron

Perceptron의 기본적인 구조는 위에 있는 그림과 같습니다. 먼저 input으로 vector형식의 데이터가 들어온다면 이것을 weight와 곱하게 되고 모든 노드들의 총합을 구하게 됩니다. 그 이후에는 합한 그 데이터를 activation 함수를 통해서 최종적으로 그 뉴런의 결과가 나오게 됩니다. 딥러닝 구조는 여러 개의 데이터가 한 번에 들어가는 vector형식을 주로 사용하며 합하게 된 값을 처리하는 activation 함수도 다양하게 존재한다.
이미지 분류 문제를 예시로 설명을 해보겠다.

손글씨 이미지 데이터를 활용해서 그 이미지가 어떤 숫자인지를 분류하는 문제라고 예시를 들어보겠다. 그렇다면 이런 이미지 데이터는 이미지의 픽셀 단위로 1열로 배열된 vector형식으로 변환이 될것이면 이 데이터는 결국 input이 된다. 그 이후에는 각각의 노드에 초기화했던 weight 값을 곱하게 된다. 그 값을 모두 지나면 activation 함수인 f를 최종적으로 지나게 되고 0~9 까지는 숫자 중 어느 class에 가장 높은 확률로 분류가 되는지 결과가 도출되게 된다.
2.1. Activation function
그렇다면 퍼셉트론에서 사용하는 activation function은 무엇이 있으며 어떤 역할을 하는지 알아보자.
이전에서 설명했던것과 같이 activation function은 다음 뉴런으로의 신호를 전달하는 신호를 결정하는 역할을 한다. 아래에 있는 그림처럼 입력되는 신호에 따라 입력신호를 그대로 반환하는 Identity function을 시작으로 0 이하의 데이터는 모두 0으로 0 이상의 데이터는 입력신호 그대로를 반환하는 ReLU 방식까지 존재한다.
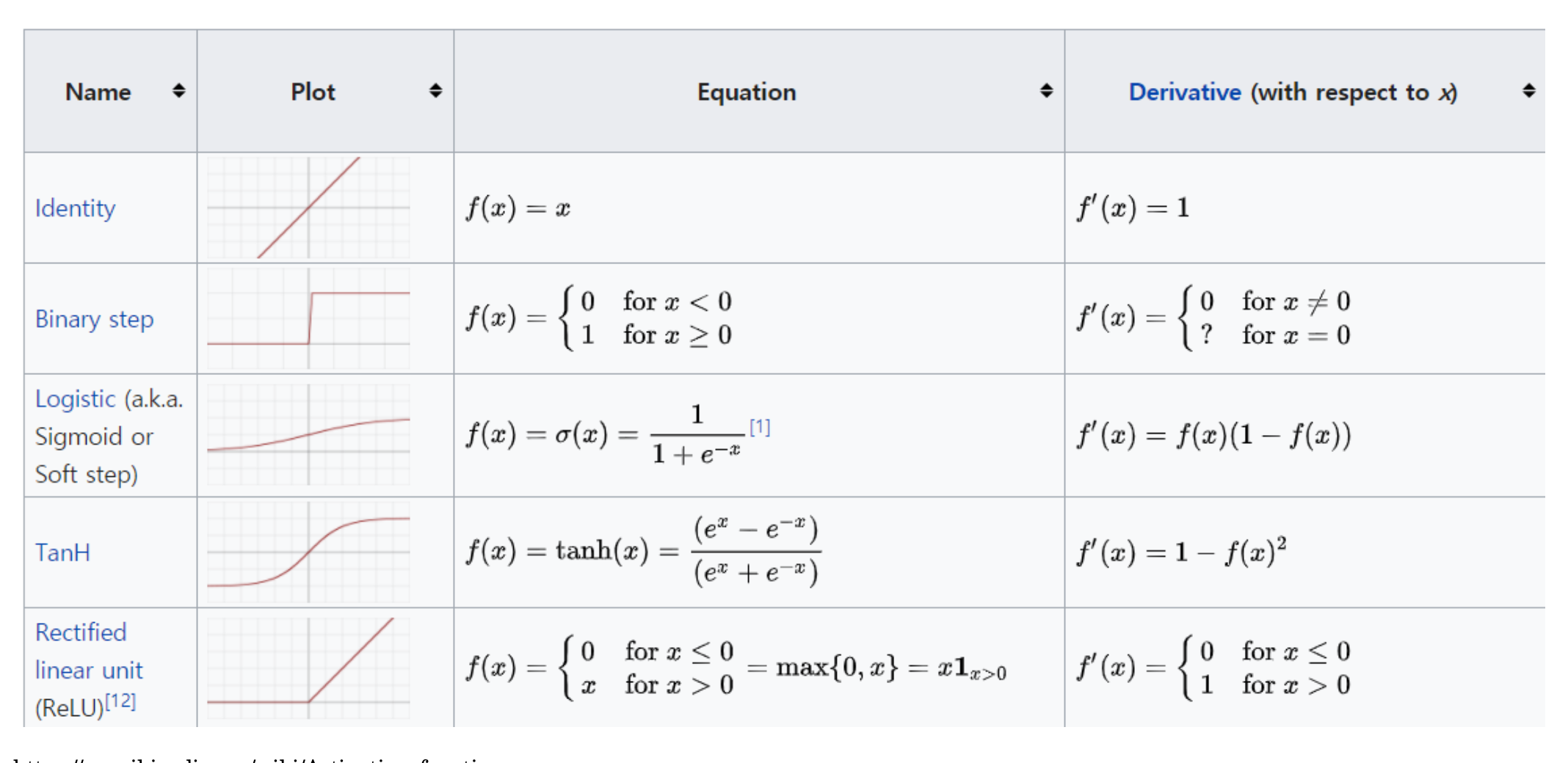
그렇다면 이런 좋은 activation function의 조건은 무엇일까?
1. Large derivative value
이후에 설명을 하겠지만 예측값과 정답과의 차리를 계산하고 파라미터를 업데이트 하는 과정에서 계산하는 gradient값을 구할 때 activation function의 미분값을 활용하는데 여러 layer를 구성하면서 미분값이 크면 gradient값이 사라지지 않는다.
2.Easy to compute derivative
미분값을 계산하기 쉬워야 한다. 이것 또한 layer가 여러개로 이루이진 구조에서 미분값을 계산할 때 계산이 쉬우면 성능에도 중요한 역할을 한다.
3.Zero-centered
좌우의 값이 0 을 기준으로 이루어진 activation function을 이야기한다.
3. Single perceptron, MLP(Multi Layer Perceptron)
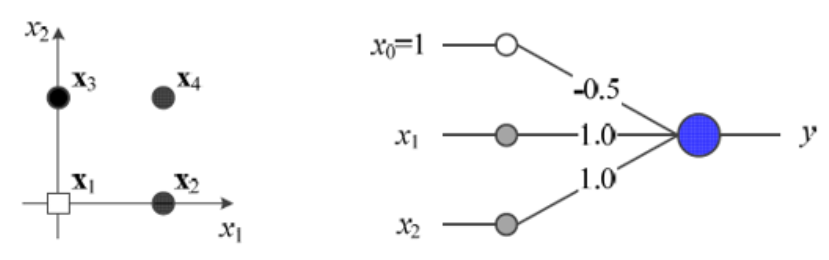
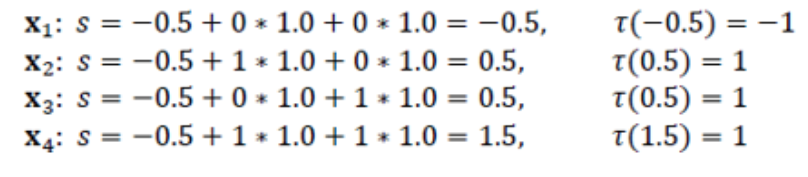
여기서 perceptron 이 작동되는 방식을 설명하자면 먼저 왼쪽의 그림에서 나오는 데이터가 입력 데이터가 있다고 가정해 보자. 그렇다면 이 데이터를 기준으로 노드에서 weight와 곱하게 되고 그것의 합을 구하게 된다. 그리고 그 값을 activation 함수에 대입하여 결국 결과를 도출한다.
여기서 activation function은 0 이상이면 1 0 이하이면 -1 을 반환하는 step function을 이용하였다. 그렇게 된다면 결국에는 -1과 1 이 분류되는 classification이 된다. 이런 방식으로 weight를 조절하면 데이터를 분류하는 classification 모델이 완성된다. 이걸 이용한다면 AND Gate와 NOT Gate를 만드는 것이 가능하다.
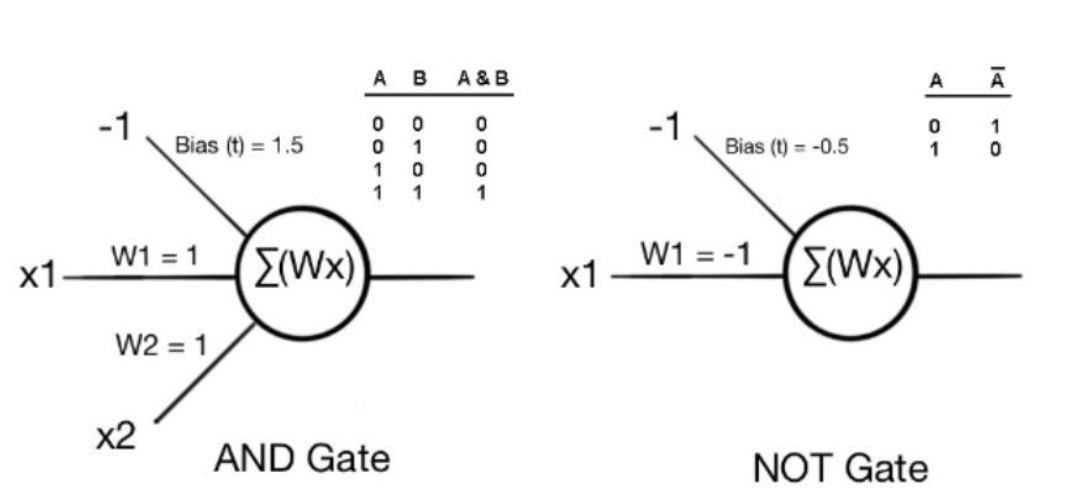
하지만 여기서 고질적인 문제가 생긴다. AND, NOT Gate를 통해서 모델을 구성하는건 가능하지만 XOR을 구분하는 방법이 없다.
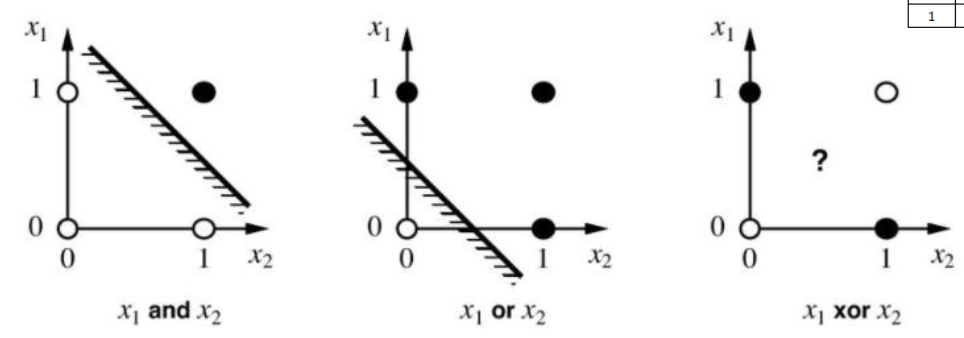
XOR문제를 해결하기 위해서 아래의 그림과 같이 Perceptron을 한개 더 추가를 해서 문제를 해결했다.
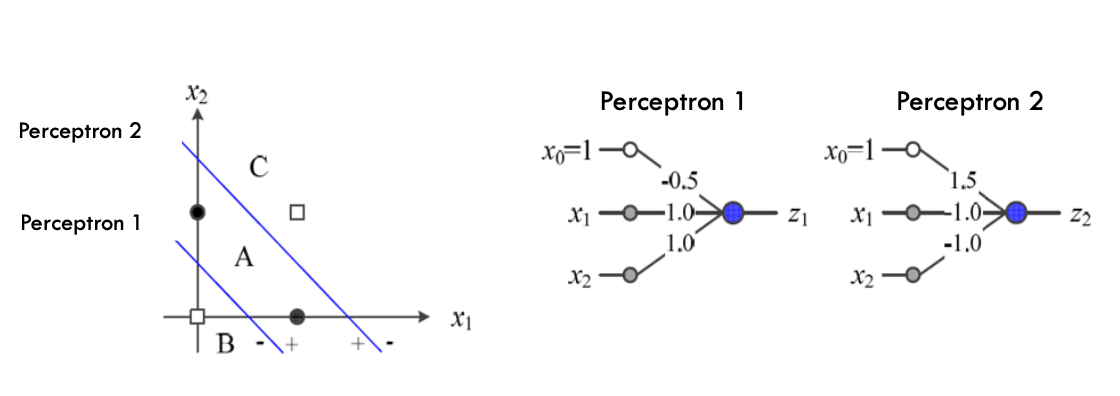
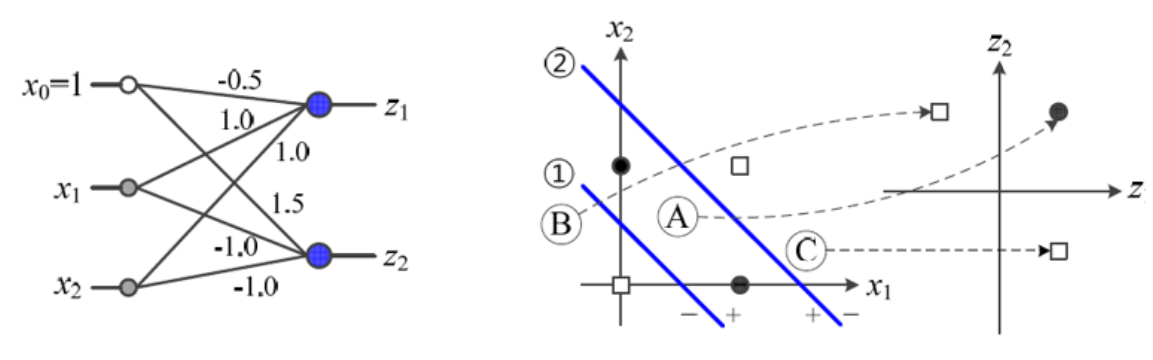
위에서 구성했던 2개의 Perceptron에서 결과값들을 이용해서 3번째 Perceptrion과 이어서 결과를 도출하게 한다.
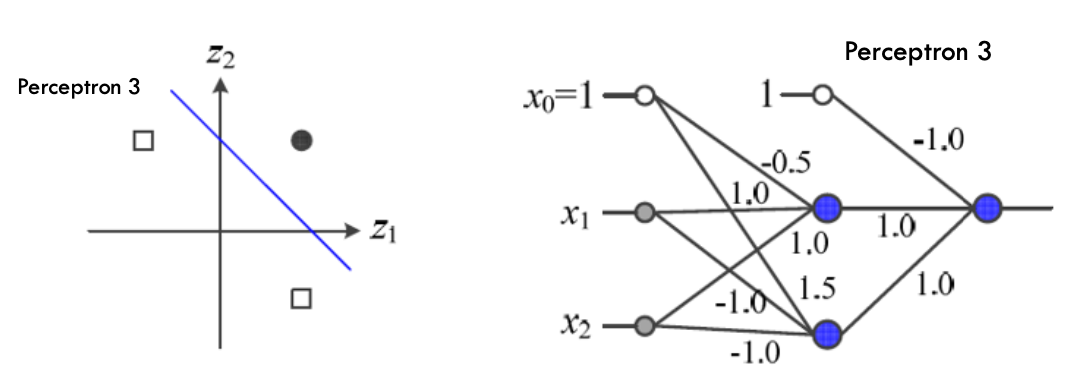
이렇게 binary classification 에 대한 기본 틀은 설명이 되었다.
그렇다면 모델의 구조가 조금 더 복잡해지고 여러개의 class를 분류하는 문제로 된다면 Perceptron의 구조는 MLP구조로 더 복잡하게 구성이 되며 우리가 아는 기본적인 딥러닝의 구조가 된다.
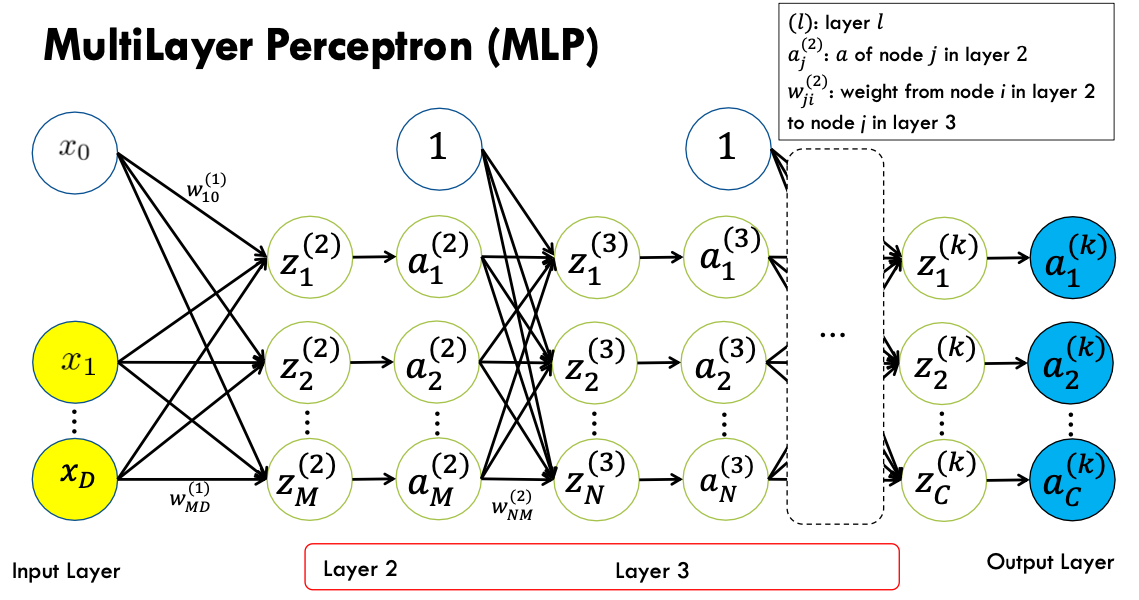
4. Backpropagation
MLP 구조에서 parameter인 weight를 업데이트 할때는 gradient를 계산해서 파라미터를 업데이트해준다. 이때 사용하는 방식이 Backpropagation이라는 방식을 사용한다.
Backpropagation을 설명하기 앞어서 Chain Rule을 설명을 해야 한다.
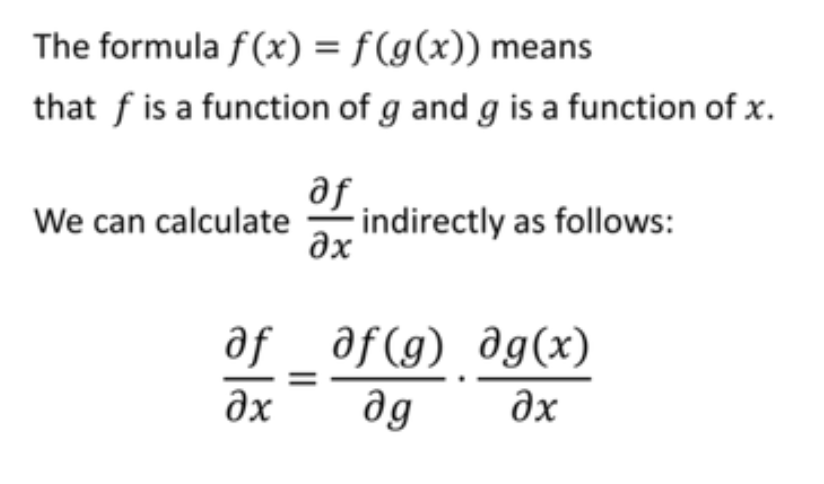
Chain rule(연쇄 법칙)은 미분의 기본적인 규칙 중 하나이다. 함수가 다른 함수의 내부에 중첩되어 있는 경우, 이 규칙을 사용하여 전체 함수의 도함수(미분)를 계산할 수 있다.
간단한 형태로 설명하면, 만약 함수f(x)가 함수 g(x)의 내부에 있고, g(x)가 다시 함수 h(x)의 내부에 있다면, f(x)를 x에 대해 미분할 때, chain rule을 사용하여 f(x)의 도함수를 계산할 수 있습니다. 즉 간단하게 말해서 여러 함수가 내부에 여러 번 존재하여서 젤 안에 있는 함수의 미분을 구하기 위해서는 외부의 미분에서부터 차례고 구하면서 미분이 가능해진다.





위에 나오는 그림처럼 MSE 방식으로 error를 구했다면 그 error 값이 그 뒤에있는 layer에도 그 gradient값이 전달된다.
결국에는 모든 weight들에 대한 gradient값이 계산되고 이것을 gradient descent 방식으로 파라미터를 업데이트하면서 train이 진행된다.
'Machine Learning' 카테고리의 다른 글
| [Machine Learning] 머신러닝에서 딥러닝까지 이론 정리 (4) - Bias-Variance & Multiclass Classification (0) | 2024.03.25 |
|---|---|
| [Machine Learning] 머신러닝에서 딥러닝까지 이론 정리 (3) - Logistic Regression & Training (0) | 2024.03.18 |
| [Machine Learning] 머신러닝에서 딥러닝까지 이론 정리 (2) (0) | 2024.03.13 |
| [Machine Learning] 머신러닝에서 딥러닝까지 이론 정리 (1) (0) | 2024.03.04 |
| [Machine Learning]PCA (1) | 2023.08.02 |




