운동하는 공대생
[Machine Learning] 머신러닝에서 딥러닝까지 이론 정리 (1) 본문
이번 이론 정리는 혼자 머신러닝 이론에 대한 총정리를 하기 위해서 작성하였습니다.
1. Introduction
Traditional Programming vs Machine Learning
기본적으로 우리가 알고 있는 프로그래밍은 프로그램을 개발하는 개발자가 프로그램에 대한 룰을 정하여 일정 데이터와 프로그램을 이용하여 결과를 도출하는 방식을 말한다. 하지만 머신러닝은 개발자가 데이터를 기반으로 데이터에 대한 패턴을 학습하여서 새로운 데이터가 입력되었을 때 결과를 도출하는 방식으로 이루어진다.
이런 머신러닝에서 데이터를 설명하는 학습 방식에는 두가지가 존재한다.
Supervised Learning vs Unsupervised Learning
Supervised Learning 은 한국어로 지도학습 이라고 한다. 단어의 뜻에 따라 데이터를 가지고 학습을 진행을 함에 있어서 모델이 예측하고자 하는 결괏값이 미리 지정되어 있는 상태를 말한다. 다시 말해 "학습에 필요한 input data x 에 대하여 그에 상응하는 결과 y 값이 존재한다"라고 할 수 있다.
여기서 y 값에 따라 여러 가지 태스크로 또 나누어지는데 y 값이 카테고리가 분류되는 그런 변숫값으로 결과를 도출해야 한다면 Classification(분류)라고 칭한다. 하지만 일반전이 연속적인 숫자를 예측하는 문제로 결과를 도출한다면 Regression(회귀)라고 이야기를 한다.
- 예시
- Classification
손글씨 데이터로 유명한 MNIST 데이터를 예로들면 어떤 숫자인지를 이미지 데이터를 활용하여서 분류하는 문제를 예로 들 수 있다.

- Regression
회귀는 집의 평수를 나타내는 데이터를 활용하여서 그 집의 가격을 예측하는 문제처럼 이런 연속적인 값을 예측하는 문제를 예로 들 수 있다.

2. Linear Regression
선형 회귀를 이전에 예시를 들었던 집값을 예측하는 데이터로 먼저 설명을 하겠다.
선형 회귀 모델은 가장 단순하면서도 데이터를 설명하는 직관적인 모델이다. 기본적인 용어를 먼저 설명을 하겠다.(이후에도 추가로 같은 용어들이 사용되니 차이를 잘 인지를 해야 한다.)

먼저 우리가 흔하게 알고 있는 수학적인 함수를 생각을 해보자. 여기서 입력하는 데이터 x축을 기준으로 데이터를 입력하면 y 결과가 나온다. 이것과 마찬가지로 linear모델을 입력하는 데이터와 파라미터의 차이로 데이터를 설명하게 된다. 여기서 말하는 입력 데이터는 x , 결과는 y 그리고 모델의 모양을 판별하는 𝝷 값들은 모델의 파라미터라고 이야기를 한다.
이렇게 함수의 형식으로 모델을 설정하는 게 가능해지며 그것은 즉 파라미터의 수가 많아지면 모델을 고도화하는 게 가능해진다. 또한 파라미터의 수가 많아진다는 이야기는 입력되는 데이터의 feature(특성) 들이 많아진다는 이야기가 된다. 이는 예시에서 나오듯이 size 뿐만 아니라 location, hight 등등 다양한 데이터의 특성들이 추가되는 게 가능하다.

위에서 나오는 식을 참고하면 데이터의 파라미터의 수가 증가하면서 feature의 수도 증가하게 된다. 이런 계산은 matrix의 형식으로 한 번에 계산이 가능하며 ∑ 를 통해서 식을 도출하는 게 가능하다.
그렇다면 이제 데이터를 잘 설명하는 파라미터 즉 모델을 만들기 위해서는 어떻게 진행을 해야 하는지를 생각해 보면 데이터와 모델의 차이를 줄여 나가는 방식을 적용해야 한다.
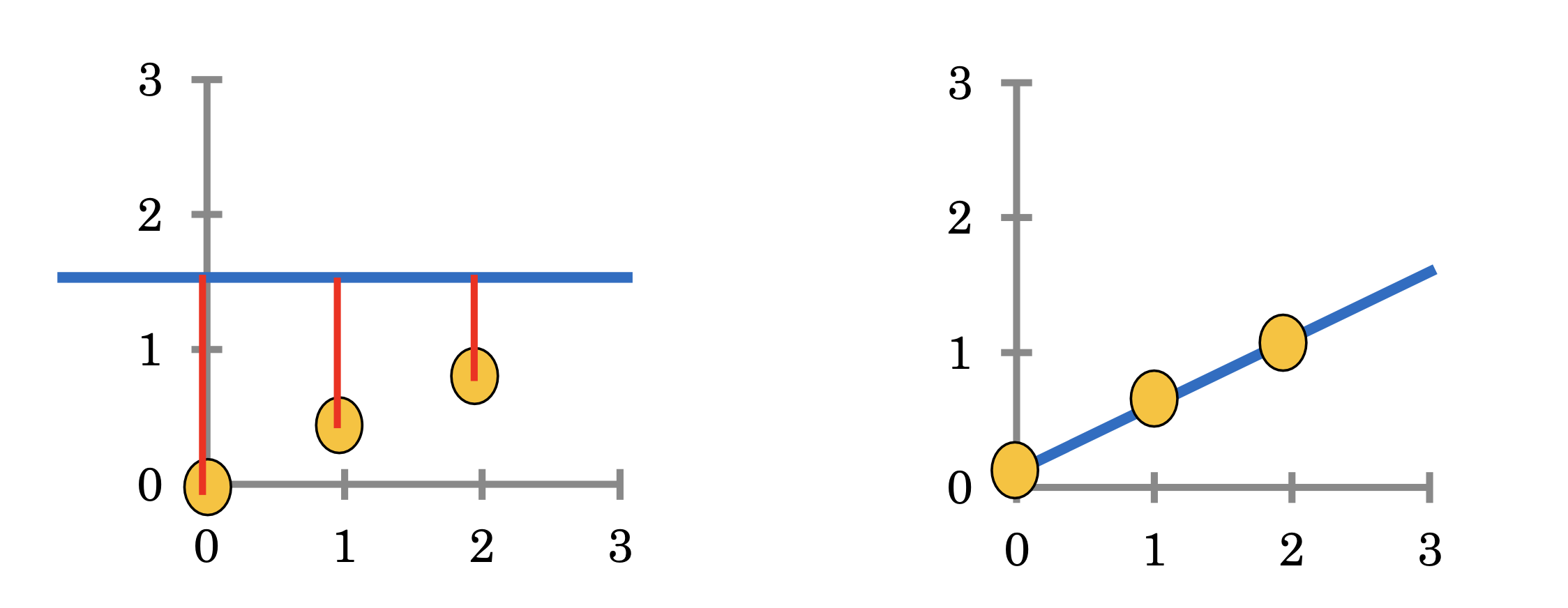
여기서 데이터와 모델의 차이를 설명하는 용어가 Error이다. Error는 실제 데이터와 모델 사이의 차이를 말하며 이것을 최소화시켜 나가는 과정을 모델의 학습 과정이라고 이야기를 한다. 또한 수식에서는 이런 Error를 Cost 혹은 Loss라고 이야기를 하며 이런 Cost를 계산하는 방식을 Cost function(J)라고 표현을 한다.
2.1 Cost Function
Cost Function는 이전에 설명을 했던 것처럼 모델과 실제 데이터 간의 차이를 계산하는 방식이다.
- Least Square Method
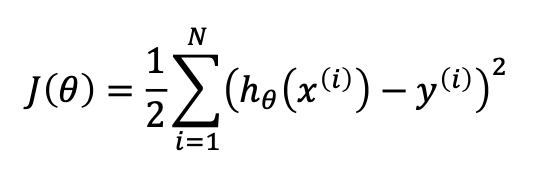
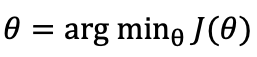
모델이 예측하는 데이터 h()에서 실제 label 데이터 y를 뺀 이후에 그것을 제곱하는 방식을 모들 데이터에 대하여 실행하게 된다. 여기서 제곱이 들어가면서 계산을 조금 더 편하게 해 주며 이런 Cost Function J를 최소화를 시키는 𝝷 를 찾는 것이 학습 과정을 나타내는 식의 과정이다. 하지만 이런 𝝷 값을 찾기 위한 방식은 어떻게 진행될까를 생각해 보기 앞서 기본적인 수학 이론을 먼저 설명을 해보겠다.
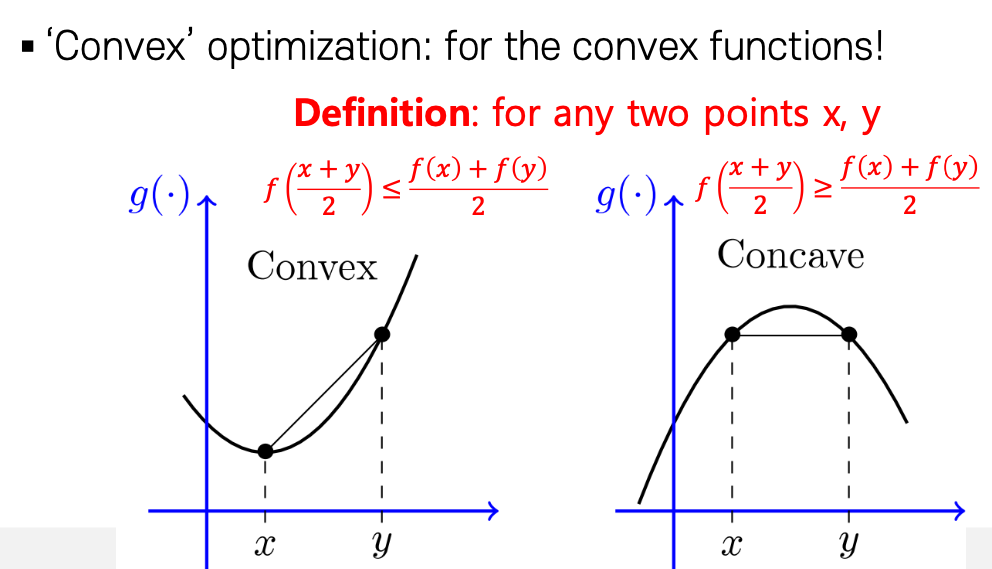
위에서 이야기했던 J 함수는 기본적으로 제곱이 들어가 있어서 2차 함수로 구성이 될것이다. 여기서 2차함수로 구성된 함수는 Convex, Concave 한 특징을 가진다. 하지만 convex일 때를 생각해 보면 어떤 함수(J)가 최소가 되려면 미분값이 0 이 되는 지점을 찾는 것을 쉽게 찾는 것이 가능하다. Convex 한 상황에서 함수가 최소가 될 가능성이 있기 때문에 Cost Function의 함수가 Convex 함을 인식을 해야 한다.
하지만 단순한 2차 방정식의 함수가 아니라 여러 개의 파라미터가 존재하여서 고차원 방정식으로 변한다면 함수에 대한 모양이 조금 더 복잡해지면서 어떤 부분에서는 Convex 하며 어떤 부분에서는 Concave 하기 때문에 이런 문제들로 일부분에서는 최소이지만 전체로 본다면 최소가 아닌 Local Minimum 문제가 발생하게 된다.
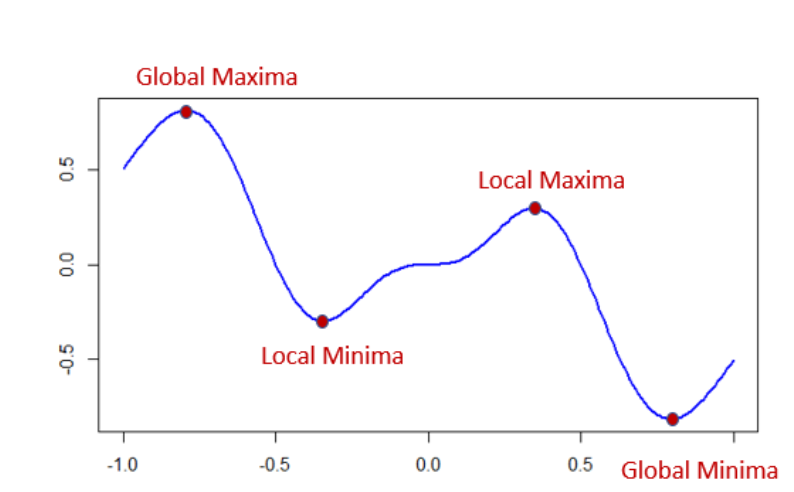
이제 다시 본론으로 들어가서 우리가 원하고자 하는 방식은 모델의 파라미터 𝝷 가 주어질 때 Cost Function의 함수를 통하여 Cost를 구하는 게 가능해졌다. 이 식을 미분하여서 최솟값을 찾는 것 또한 알게 되었다. 하지만 여기서 단순히 2개의 feature가 아니라 여러 개의 feature가 존재한다면 모든 feature에 대하여 미분하여서 계산을 해주어야 한다. 그리고 최소가 되려면 기존에 가지고 있던 파라미터의 값을 수정을 해나가야 하는데 여기서 이 방식에서도 새로운 이론이 등장하게 된다.

그 방식이 바로 Gradient Descent 방식이다. Cost Function에서 파라미터를 기준으로 미분을 진행한 값을 gradient라고 하는데 이 값을 이용하여 기존에 있던 파라미터 값을 조정을 해나간다.

위에 나오는 식처럼 Cost Function J를 특정 파라미터를 기준으로 미분하고 Learning Rate 𝜶 값을 곱하여 기존에 있던 파라미터에서 빼주어 새롭게 파라미터의 값을 업데이트한다. 이렇게 된다면 파라미터의 값이 점점 변경되게 되며 파라미터의 변화가 거의 없을 때까지 모델이 업데이트가 된다. 이렇게 된다면 데이터를 가장 잘 설명하는 모델이 학습되게 된다.
여기서 주의해야 할 점은 특정 파라미터 값을 업데이트하고 다른 파라미터를 업데이트하는 방식이 아니라 모들 파라미터에 대하여 gradient 값을 계산을 하고 그 이후에 파라미터를 각각 업데이트를 시켜준다.
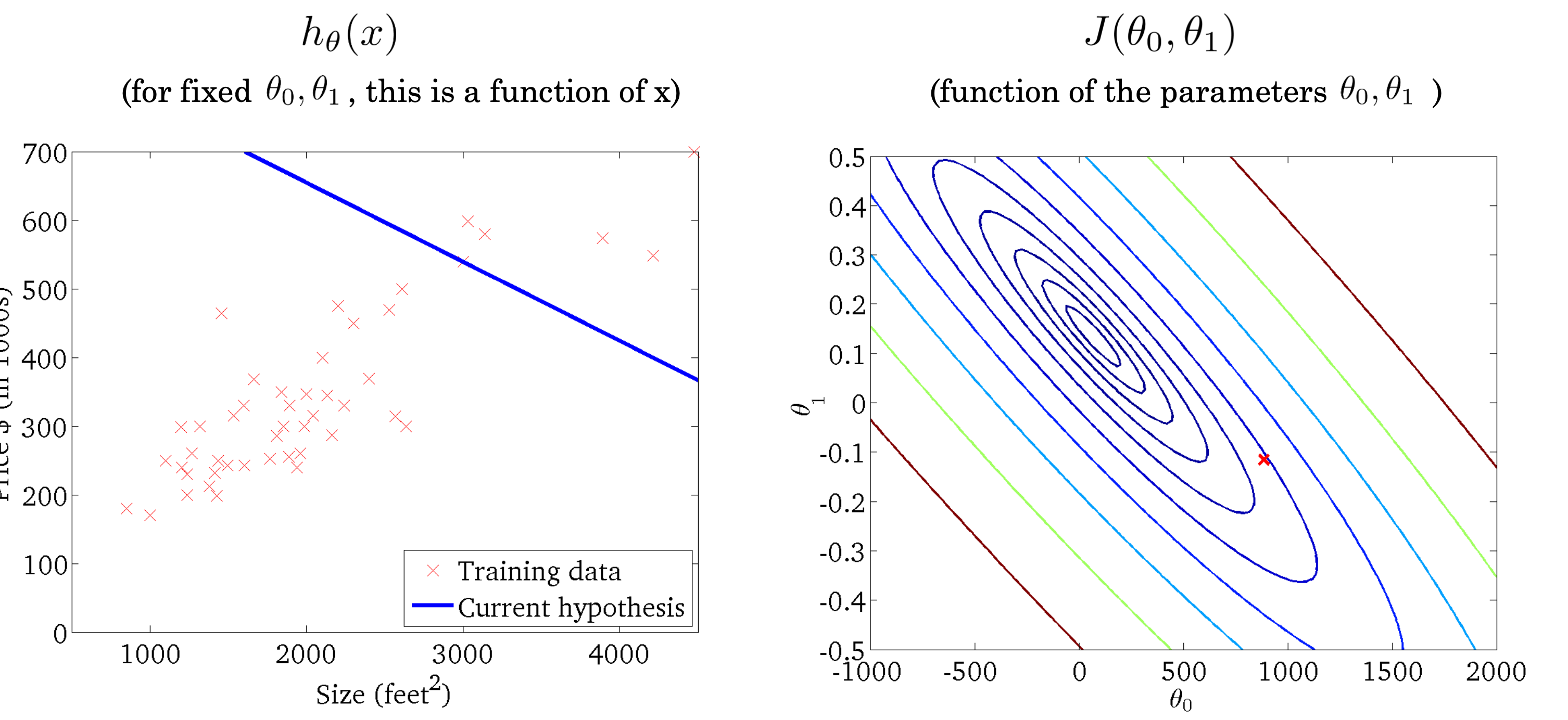
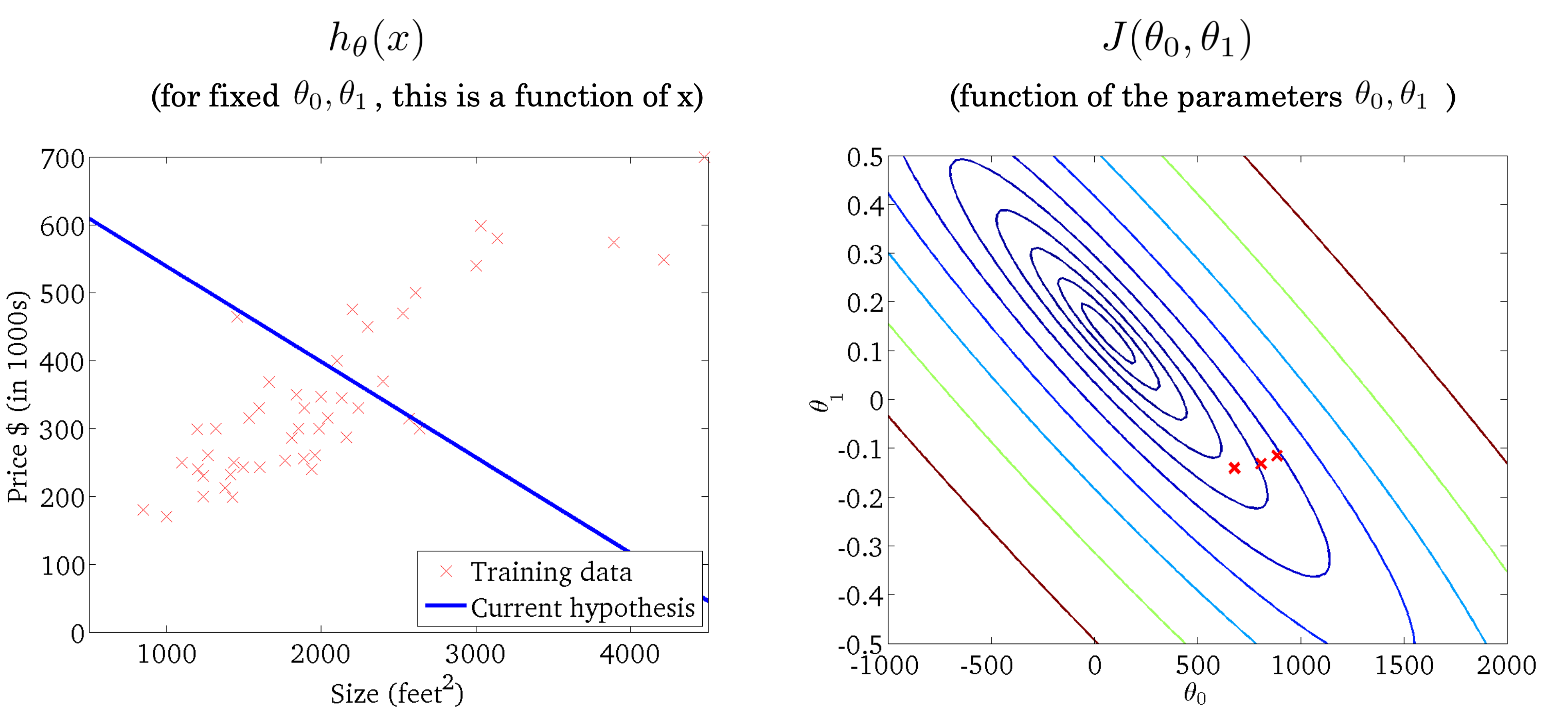
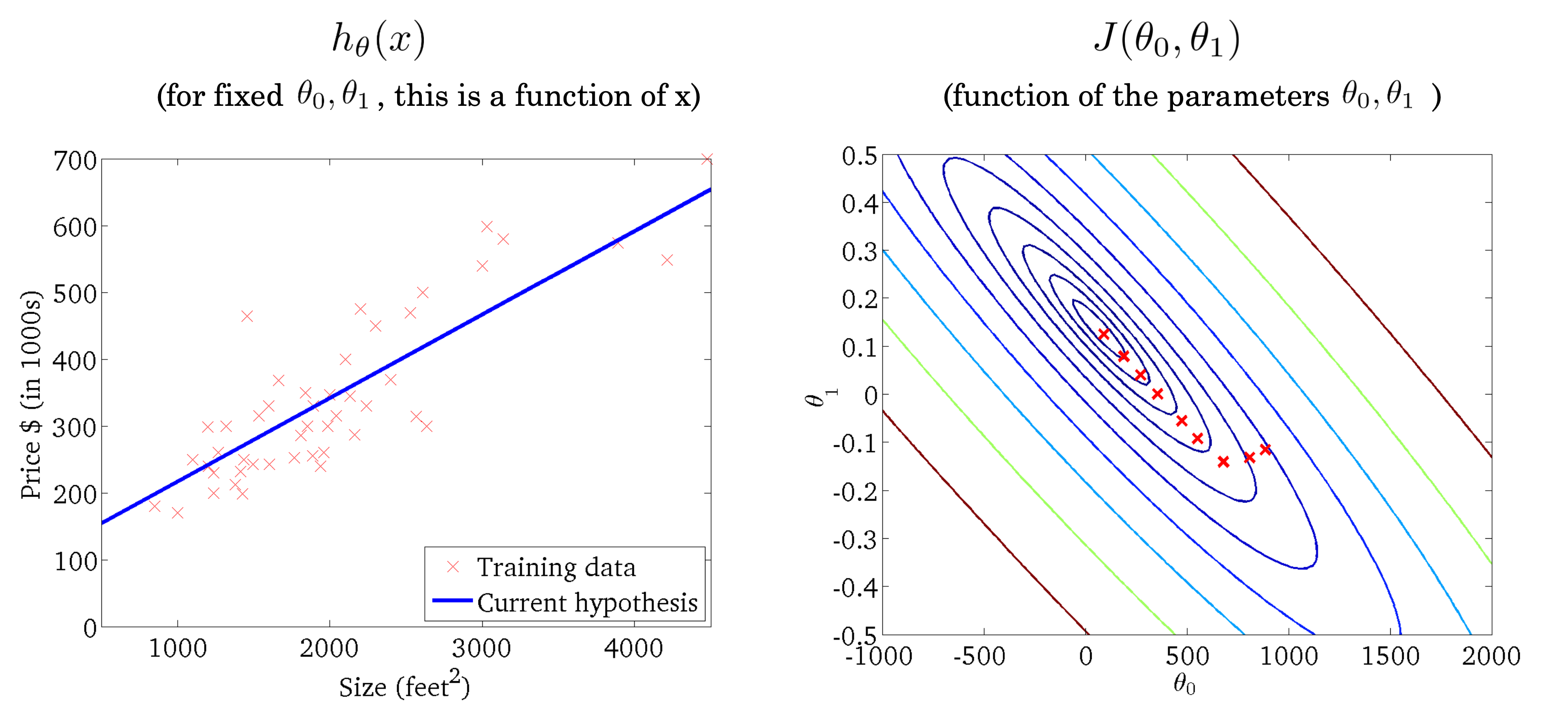
2.2 Batch
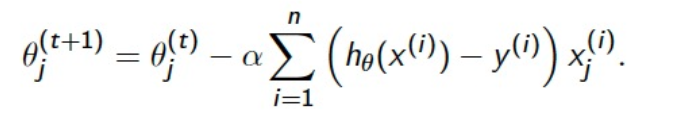
2.1에서 설명했던 parameter update방식에서 Cost Function을 다시 풀어서 작성하면 위의 식처럼 전개가 가능하다. 여기서 n 은 이전에 가지고 있는 모든 데이터라고 이야기를 했다. 하지만 여기서 이 값을 조정하는 방식을 Batch라고 이야기를 한다.
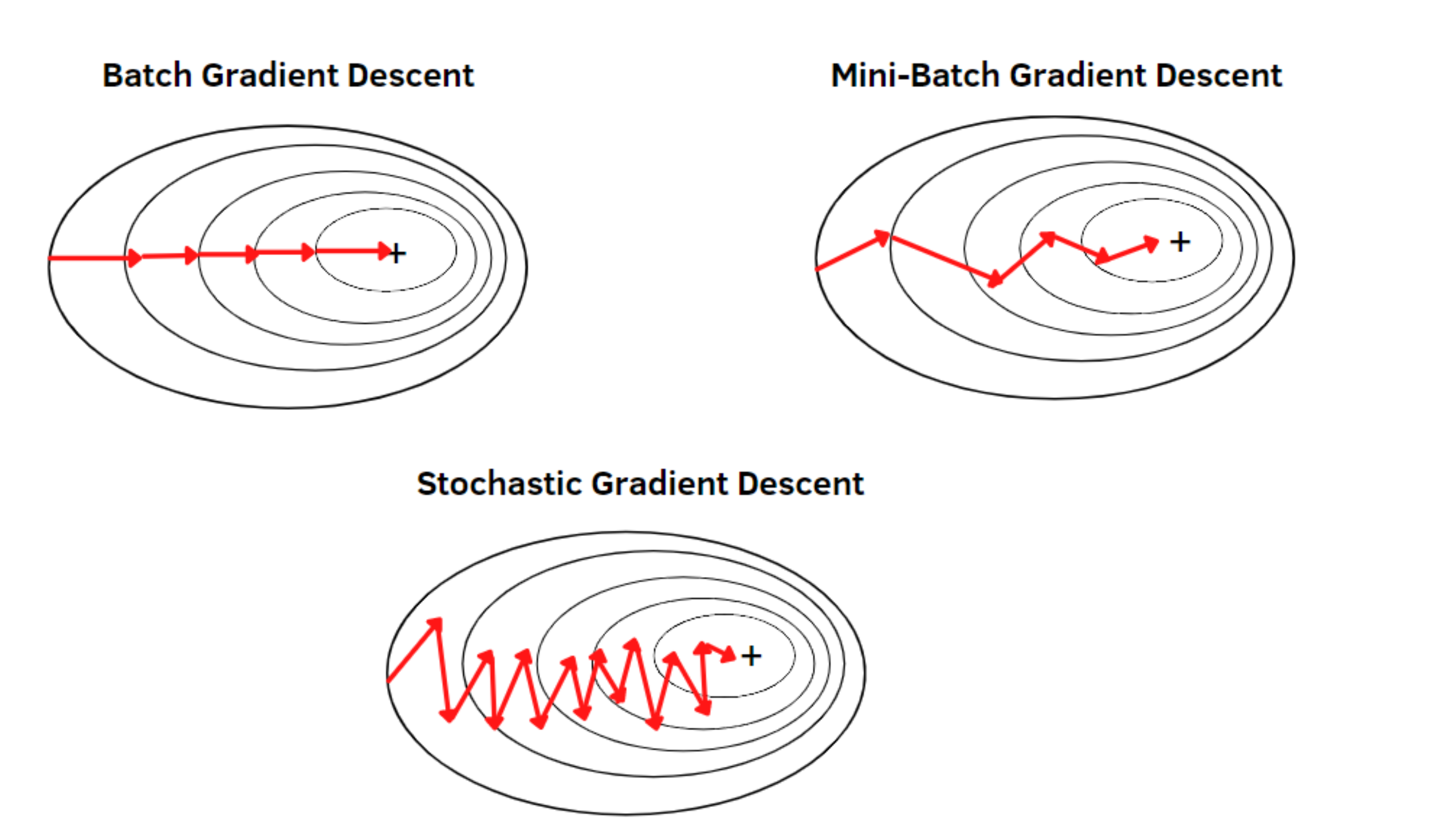
즉 여기서 Batch라는 말은 파라미터를 업데이트할 때 몇 개의 데이터를 가지고 파라미터를 업데이트할 것인지를 정하는 말이다. 모든 데이터마다 파라미터를 전부 업데이트를 한다면(데이터의 수가 n=100이라고 가정한다) n=1 Stochastic Gradient Descent(SGD) , n= 10 Mini-Batch , n=100 Batch 이렇게 Batch를 나눠서 파라미터를 업데이트하는 방식들이 있는데 일반적으로 Mini-Batch방식이 가장 많이 사용되며 Batch를 나누게 된다면 Local minimum 문제를 해결하는데 도움이 된다.
2.3 Polynomial curve fitting
더 나아가 이전에서의 단순한 simple linear function 이 아니라 다항함수의 구조로 변한다면 어떻게 바뀌는지를 이야기를 해보겠다.
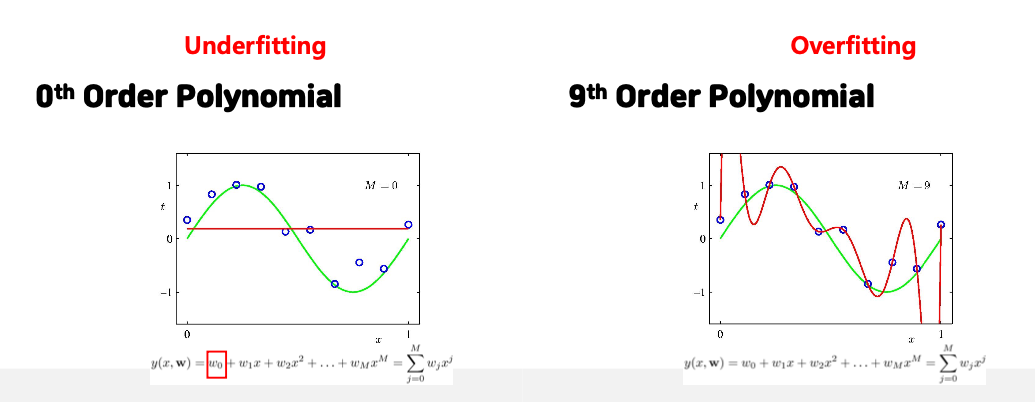
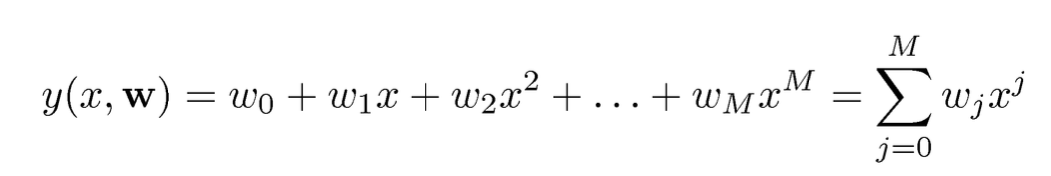
위의 식에서 보이듯이 함수의 차수가 높아지면 모델의 구조는 조금 더 복잡해지며 복잡한 데이터를 설명함에 있어서 더욱 고도화된 모델을 만드는게 가능하다. 하지만 그림에서 보여지듯이 너무 고차원의 함수 구조는 오히려 성능이 낮아지는 문제가 발생한다. 즉 모델이 데이터를 설명함에 있어서 학습 데이터를 너무 치중하여 복잡한 구조의 모양으로 학습되면서 새로운 데이터를 입력받았을 때 성능이 급격하게 하락하는 모습을 보이게 된다. 여기서 데이터에 대한 학습이 너무 많이 이뤄져 있는 상태를 Overfitting(과적합)이라고 이야기를 한다. 반대로 너무 데이터에 대한 학습이 이루어지지 않은 상태를 Underfitting(과소적합)이라고 이야기를 한다.
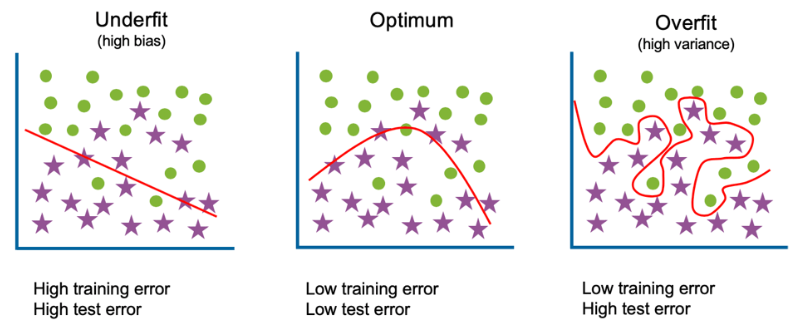
Overfitting에 대한 문제는 모델에 대하여 심각한 문제로 작용한다. 이런 문제를 해결하기 위해서는 보통 2가지 방법을 사용한다.
- Train more data : 데이터를 더 추가하여서 모델이 더 잘 구분을 하도록 하는 방법
- Regularization : Regularization term을 사용하여서 급변하는 파라미터의 업데이트를 방지한다.
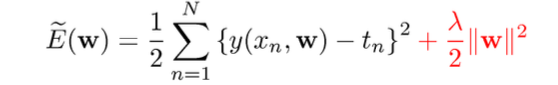
'Machine Learning' 카테고리의 다른 글
| [Machine Learning] 머신러닝에서 딥러닝까지 이론 정리 (3) - Logistic Regression & Training (0) | 2024.03.18 |
|---|---|
| [Machine Learning] 머신러닝에서 딥러닝까지 이론 정리 (2) (0) | 2024.03.13 |
| [Machine Learning]PCA (1) | 2023.08.02 |
| [Clustering]Maximum Likelihood Estimation-최대우도법 (0) | 2023.07.25 |
| Automated Machine Learning (AutoML) (0) | 2023.05.12 |




