운동하는 공대생
[Machine Learning] 머신러닝에서 딥러닝까지 이론 정리 (3) - Logistic Regression & Training 본문
[Machine Learning] 머신러닝에서 딥러닝까지 이론 정리 (3) - Logistic Regression & Training
운동하는 공대생 2024. 3. 18. 13:591. Logistic Regression

Linear Regression 모델을 이제까지는 알아봤는데 여기서 Regression이라는 태스크는 연속적인 데이터를 예측하는 문제이고 Classifiction이라는 태스크로 넘어가면서 이제는 더 이상 연속적인 값을 예측하는 문제가 아닌 카테고리를 분류하는 문제로 바뀐다.
여기서 이제 일반적인 Linear 모델의 구성 방식으로는 Classification 문제를 해결하기란 쉽지 않다. 왜냐하면 Classification 문제로 넘어가면서 결괏값이 0, 1 같은 이런 값으로 떨어지게 되는데 Linear모델을 활용하면 카테고리를 분류하기가 쉽지 않다.
이로 인하여 Classification 문제를 푸는 문제에서 처음으로 제시되는 방법이 Sigmoid 함수를 활용한 방식이 등장하게 된다.
2. Parameter update


로지스틱 회귀는 기본적으로 선형 기저 함수에 시그모이드 함수를 적용한 형태이다. 이를 통해 0과 1 사이의 값으로 반환되며, 이는 확률 값으로 해석될 수 있다. 로지스틱 회귀의 목표는 입력 변수와 출력(타깃) 변수 간의 관계를 설명하는 것이며, 이를 통해 적절한 모델 파라미터를 찾는 것이 중요하다.
여기서 이제 파라미터를 업데이트 하는 과정은 LSM를 사용하지 않는다. 이유를 식으로 설명을 하자면

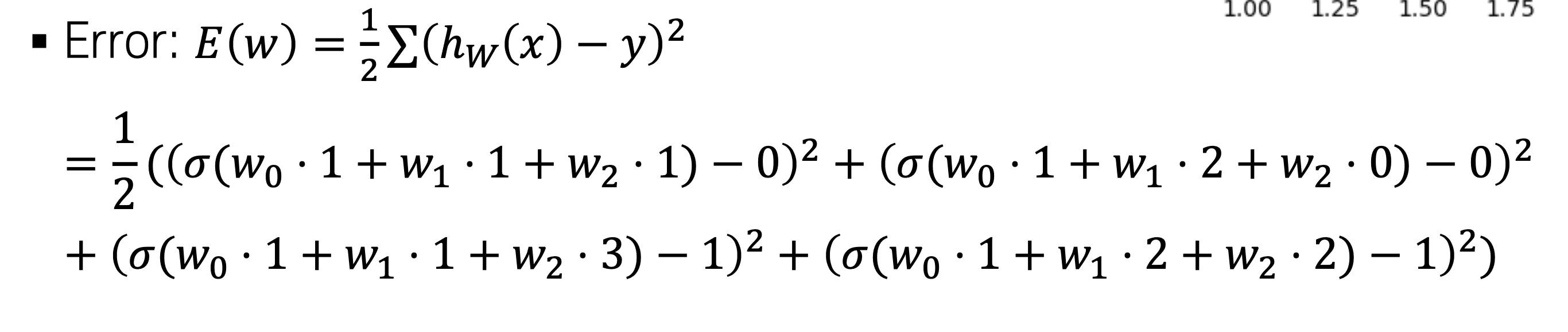
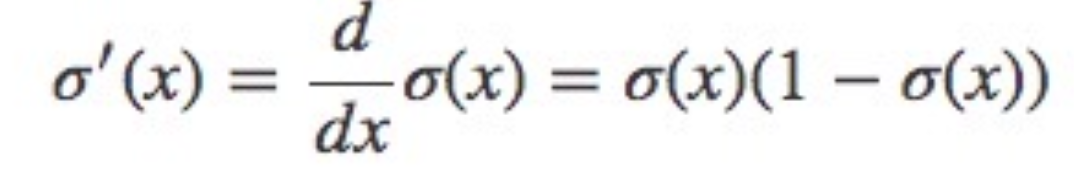
LSM 방식을 활용하여서 gradient값을 계산함에 있어서 Sigmoid를 미분하여서 계산을 하게 되는데 결국에는 원래 값으로 다시 나오는 형태로 바뀌게 된다. 함수의 변화량을 보는 것이 아니라 함수 자체로 표현이 되기 때문에 gradient 값을 계산하는 것에 문제가 생긴다.
또한 값을 계산한다고 하더라도 예측값과 label 값의 차이를 계산하는 방식에서 0과 1 사이의 값을 사용함으로 잘못 예측한 데이터라고 하더라고 loss 값이 크지가 않다.
그래서 보통은 MLE 방식을 주로 사용하게 된다.
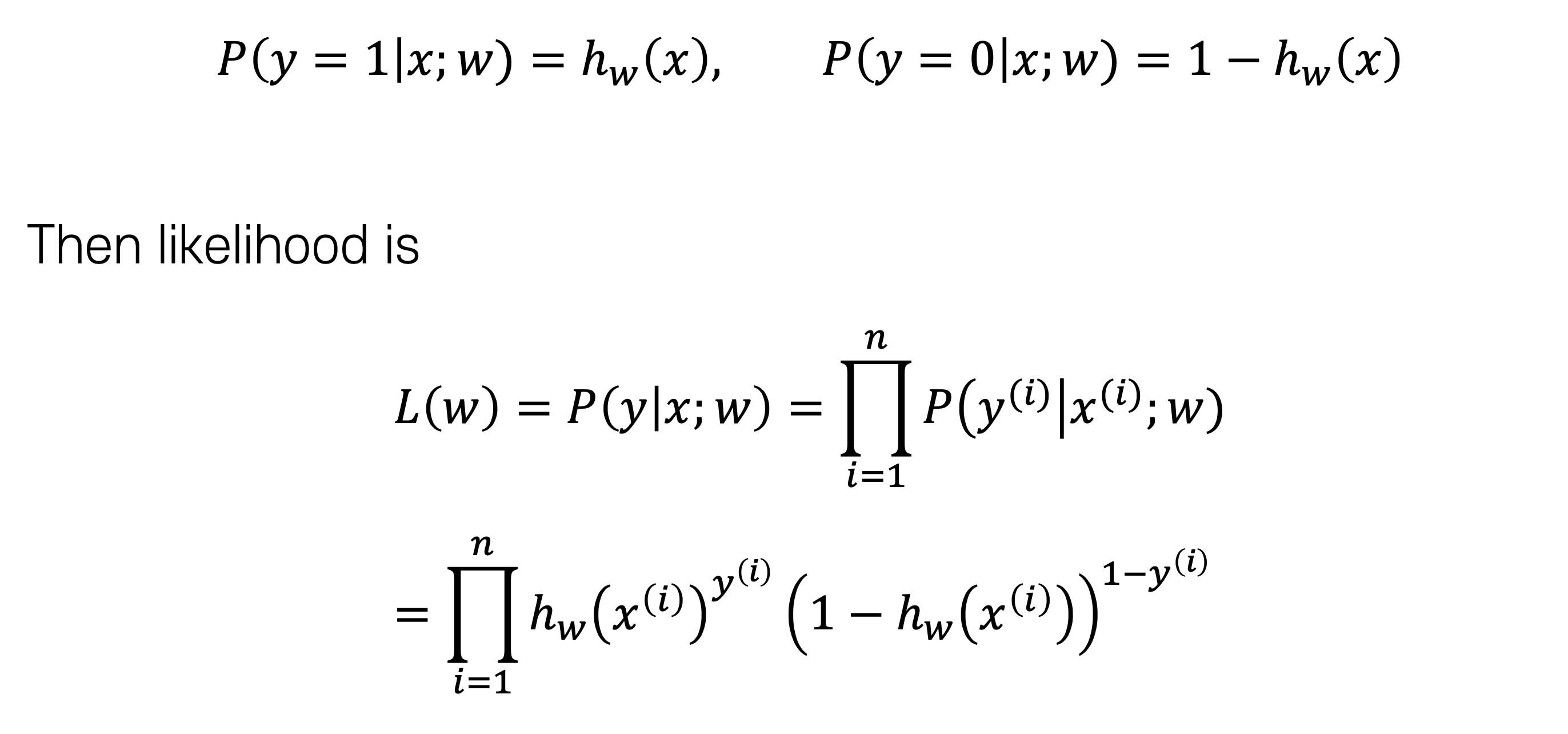
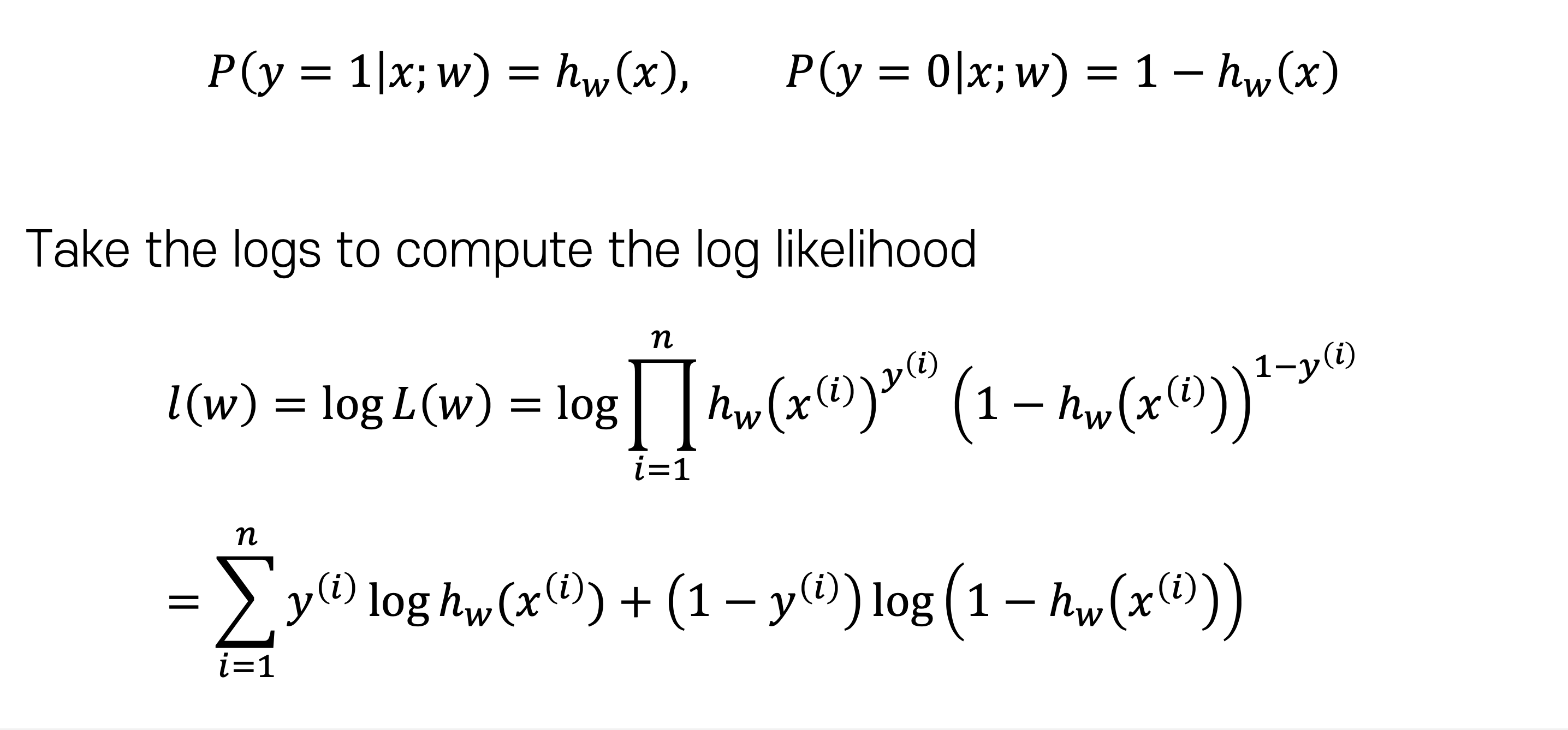
MLE 방식에서는 확률값을 활용하여서 데이터 전체에서의 확률값을 곱하게 된다. 그리고 이 값에서 log 값을 취하게 된다면 합으로 바뀌게 되면서 기존에 설명했던 loss 구하는 방식이 된다.
이제 여기서 식을 자세하게 관찰해보면 y 값에 따라서 식이 다르게 작동하는 걸 볼 수 있다.
y 값이 0이라면 뒷쪽의 식이 사용되고 y값이 1이라면 앞쪽 식이 사용되는 것을 알 수 있다. 이것을 활용하여서 Logistic regression 함수에서 사용되는 Cost Function 은 아래와 같이 정의된다.
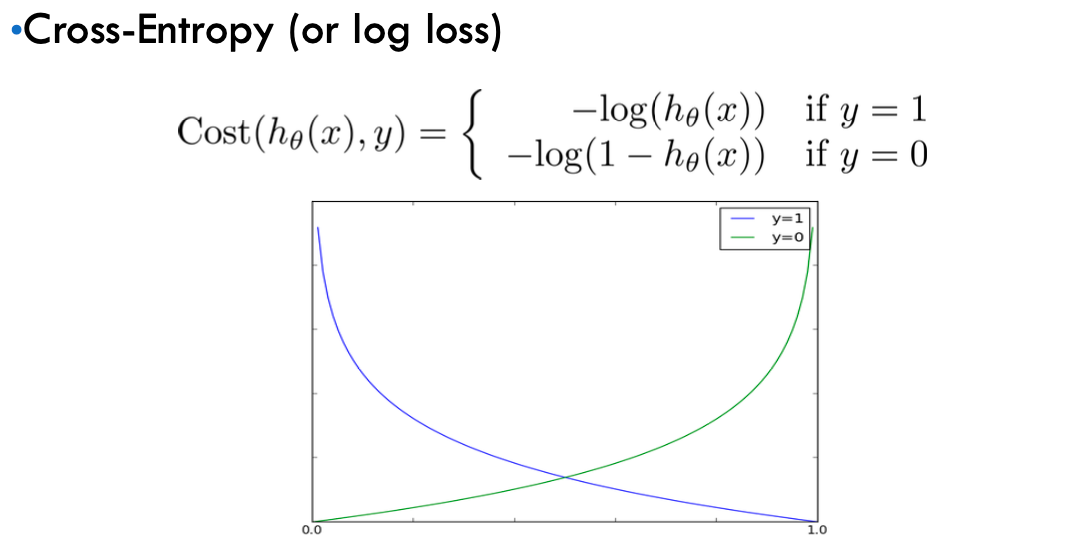
Cross - Entropy loss의 장점을 loss 값이 틀려도 적은 LSM 방식의 단점을 보안해 준다. 값을 잘못 예측하게 된다면 큰 loss값이 발생하게 된다.
그렇다면 이 Cost Function 으로 parameters를 훈련하는 과정은 어떻게 될까??
이전에 설명했던 Gradient 방식을 사용하면 최적화하는 게 가능하다.
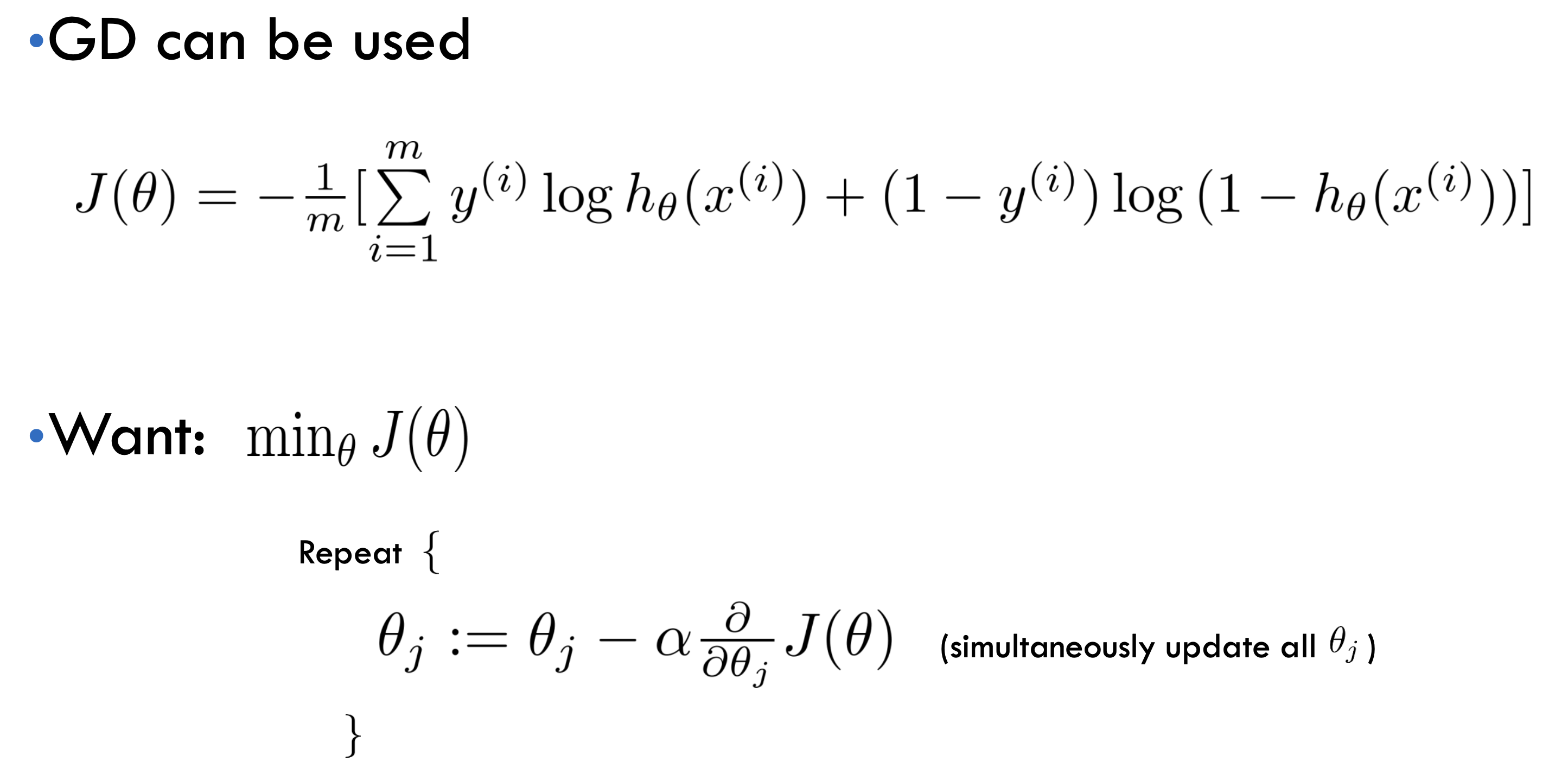
이전에 했던 방식처럼 Cost Function에 대한 미분값으로 Gradient를 계산하고 Learning Rate를 곱한 값을 이번에 파라미터의 값에서 빼준다.
이렇게 Cost 를 구하는 함수는 달라졌지만 계산은 똑같이 진행이 된다.

미분한 식을 전체적으로 전개를 해보면 이전에 Linear Regression Gradient 방식에서와 차이점은 basis funcation 즉 h(x) 함수가 다르다는 점이다.
'Machine Learning' 카테고리의 다른 글
| [Machine Learning] 머신러닝에서 딥러닝까지 이론 정리 (5) - Perceptron, Backpropagation (0) | 2024.04.08 |
|---|---|
| [Machine Learning] 머신러닝에서 딥러닝까지 이론 정리 (4) - Bias-Variance & Multiclass Classification (0) | 2024.03.25 |
| [Machine Learning] 머신러닝에서 딥러닝까지 이론 정리 (2) (0) | 2024.03.13 |
| [Machine Learning] 머신러닝에서 딥러닝까지 이론 정리 (1) (0) | 2024.03.04 |
| [Machine Learning]PCA (1) | 2023.08.02 |




