[논문] Deep Learning and the Information Bottleneck Principle

https://arxiv.org/abs/1503.02406

Deep Learning and the Information Bottleneck Principle

1. Introduction

   논문에서는 현재 많이 사용하고 있는 딥러닝 분야에서 가장 중요한 부분인 몇 개의 layer를 사용할 것이냐를 두고 이야기를 했다. 또한 딥러닝 모델의 layer가 늘어남에 있어서 RG(Renormalization Group)이라는 현상이 더욱 두드려지게 되는데 이는 layer가 깊어지면서 특징을 더 잘 추출한다는 이야기를 하면서 예측과 압축(추출) 에는 tradeoff 가 존재한다고 이야기를 한다. 

 

이러한 특징 대문에 input variable에서는 최대한의 많은 정보를 압축을 하면서도 output variable에 대한 정보 또한 보존하고 있어야 한다고 한다. 이것이 IB(Information Bottleneck) 이론에서 다루는 조건이다.

논문에서는 이런 layer 들의 데이터의 과정을 Markovian 구조를 통해서 통계적으로 이전 layer의 데이터를 기반으로 다음 layer에 어떻게 영향을 미치는지, 그리고 어떻게 이전 layer의 정보를 얼마나 담고 있는지 등을 표시하기 위해서 Markovian를 사용하였다.

 

추가로 이것을 통해 얼마나 많은 데이터를 학습해야 모델의 학습이 잘 이루어 지는지 그런 것도 표현하는 게 가능해진다.

논문에서 또 중요하게 다룬 문제는 딥러닝 모델이 비선형적 특성을 가짐으로서 복잡한 패턴을 분류, 예측하는 게 가능하다는 점을 주목했다. 이런 특성으로 hidden layer 구성이 더욱 필요로 하게 되었으며 데이터를 설명함에 있어서 반드시 필요한 구조라고 이야기를 했다. 그래서 이런 비선형적 특성을 가지는 것이 IB의 변화와 관련이 있음을 이야기를 했고 이런 변화를 통해서 모델의 복잡도를 파악하는 게 가능하다고 이야기를 한다.

 

2. Background

2.1 Deep Neural Networks

   딥러닝에서 모델이 데이터를 분류 하기 위해서는 입력 데이터와 예측하려는 데이터 즉 label 사이에 독립적으로 존재를 해야 하는데 이는 두 변수들 간에 상관관계가 없어야 한다는 이야기이다. 이것을 입력 x에 대한 베이즈 정리를 사용해서 나타내면 아래와 같이 나타내는 게 가능하다. 즉 x에 대하여 y의 조건부 확률을 타내는데 이것을 시그모이드 함수를 이용하여서 식을 구성하고 각각의 데이터에 대한 확률값을 모두 곱하여 값을 계산한다.

여기서 뉴런의 weight 를 wj = log p(xj |y) p(xj |y0) ,  bias를 b = log p(y) p(y0) , hj = np(xj )를 각 layer의 입력 데이터라고 생각하는 게 가능하다. 모델을 학습하면서 특징을 추출하여 단순화하는 문제로 변환하는 RG 변환을 진행하고 RBM 방식으로 각각의 뉴런 간의 결합을 모델링합니다.

 

2.2 The Information Bottleneck Principle

    Information bottleneck(IB)를 입력확률 변수에서 데이터를 추출하고 출력 랜덤 변수에서의 정보를 가지고 있다. 이것을 X. Y라고 한다면 p(X, Y)로 표시가 가능하다. 그리고 관련한 정보는 상호 간의 관계를 I(X;Y)로 표시하여 정의한다 그렇다면 이제 예측을 하려는 정보를 가지기 위해서 입력 데이터의 특징을 추출하여 사용을 해야 하는데 여기서 입력 정보의 최소한의 정보를 가지게 해야 하므로 I(X;X^)의 관계가 최소화가 되어야 한다. 이런 관계를 한 번에 표현하기 위해서 Markov chain을 사용하면 Y -> X -> X^ 의 형식으로 사용된다.

 

결과적으로  I(X;X^) 이라는 조건을 최소화하려는 목적을 가지고 있을 때 특정 조건인  I(X;Y) 를 이용하여 식을 구한다면 라그랑지를 활용하여 표현하는 게 가능하다. 

Kullback-Leibler (KL) 발산과 rate-distortion와는 밀접한 관련이 있는 개념이다. KL 발산은 두 확률 분포 간의 차이를 측정하는 방법 중 하나로, 정보 이론에서 사용된다. Rate-distortion 문제는 데이터 압축과 정보 손실 간의 균형을 찾는 문제이며, KL 발산은 rate-distortion 문제에서 왜곡(distortion)을 측정하는 데 사용된다.

d: Kullback-Leibler divergence
=> 확률 분포 간의 유사성 또는 차이를 측정하는 정보 이론에서 사용되는 개념입니다. 이것은 두 확률 분포 P와 Q 사이의 차이를 나타내며, 두 확률 분포가 얼마나 다른지를 측정하는 도구로 사용됩니다.

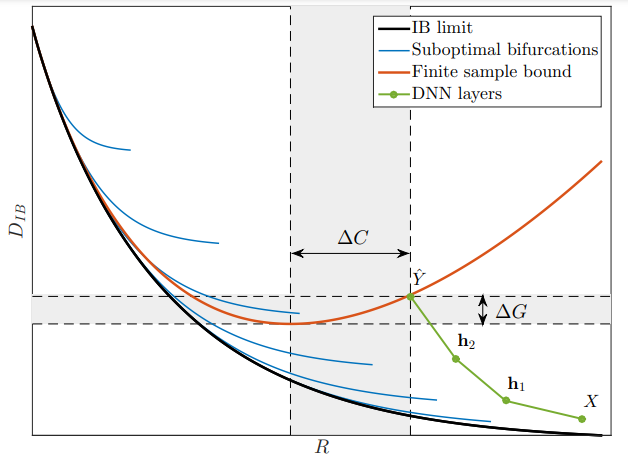
R 값은 입력 데이터의 복잡성 또는 데이터 표현의 정보량을 나타낸다.

 

 

3. A New Information Theoretic Learning Principle for DNNs

3.1 Information characteristics of the layers

    DNN에서 layer의 특징은 이전 layer의 데이터가 전달받으면 다음의 layer로 전달된다. 또한  Y를 예측하기 위한 정보가 손실된다면 더 깊은 layer에서 이것을 회복하는 게 쉽지 않다. 더 깊은 layer를 j로 한다면 i >= j로 표현한다.

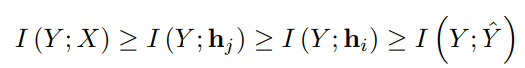
h는 layer의 결과로 layer를 지나가면 지나갈수록 Y를 예측하는 정보들은 충분히 담고 있어야 한다. 그리고 각각의 layer의 값은 Y와 I 값이 최대가 되어야 하며 각각의 layer 끼리의 h 값은 최소화가 되어야 한다. 즉 layer를 지날 때 데이터가 같아지는 걸 최소화해야 한다. 중복을 최소화해서 모델의 효율성을 높이기 위해서.

 

그래서 이런 장점은 각각의 hidden layer 끼리의 성능도 평가하는게 가능하다. 이것 또한 라그랑지 방식을 통해서 수치적으로 계산하는 게 가능하다. 그래서 기존에 error를 측정했던 방식과 다르게 은닉층에서의 성능 평가가 가능하다. 그래서 위에 나왔던 그래프의 DNN 구조에서 hidden layer의 수치도 표시가 되어있다.

 

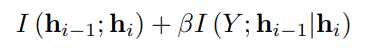
3.2 Finite Samples and Generalization Bounds

    제한된 수의 학습 데이터에서 학습을 진핼할때 이제까지 설명했던 mutual information에 대한 수치를 어떻게 해석을 하는지를 이야기를 하고 있다. 

 

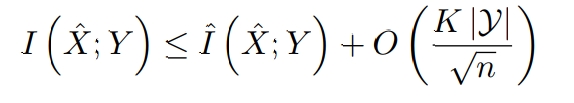
먼저 최소한의 정보 y 에 대한 정보를 가지며 x에 대한 정보를 추출한 x^ 을 통해서 상호 간의 관계에 대한 정보가 얼마나 있는지를 Y와 비교를 하였을 때 이는 모델의 입력 변수의 입력 가능한 수 를 K라고 하고, 출력 변수에서 출력될 수 있는 가능한 수를 y라고 한다면 이것을 데이터 샘플의 수로 나눠서 가능한 모델의 오차를 일반화하여 더하게 된다. 그렇게 된다면 모델의 가지고 있는 일반화 오차의 상한선을 계산하는 게 가능하고 이것을 너무 많이 넘게 되면 과적합 문제를 발생한다는 기준을 만들어준다.

 

K= 2^I(X^;X) 로 표현이 된다. 이것은 복잡성을 나타내는 K 가 X^ 가 X에 대한 얼마나 많은 정보를 담고 있는지에 대하여 그 값을 정의하는 게 가능하다.

 

요약하면, 모델의 입력 레이어만으로는 일반화에 부족하며, 정보의 압축(compression)과 요약이 필요하다는 점을 강조하고 있다. 딥 뉴럴 네트워크에서는 입력 데이터를 적절하게 처리하고 변환하는 과정이 중요하며, 이를 통해 모델이 새로운 데이터에 대해 더 잘 예측하고 일반화할 수 있다.

 

이제 그럼 성능 평가를 함에 있어서 차이 즉 얼마나 좋은 성능을 나타내는지에 대한 수치를 어떻게 계산을 하는지에 대하여 이야기를 하겠다.

 

 - Generalization gap

output layer 의 D 값을 Dn이라고 한다면 현재의 layer의 D 값의 차를 통해서 실제로 네트워크의 한 layer 가 정보를 잘 압축하고 있는지를 판단하는 게 가능하다. 즉 모델의 출력인  y 값에 비해 얼마나 활용 가능한 정보를 잘 담고 있는지 판단하는 지표가 되며 과적합에 대한 지표가 된다.

 

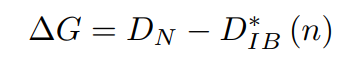
 - Complexity Gap

이것은 모델의 복잡성이 불필요하게 커지면 커지는 값으로 모델의 복잡성을 성능을 평가하는 지표가 된다.

 

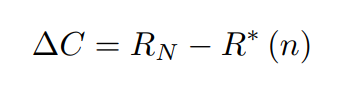
4. IB Phase Transitions and The Breakdown of Linear Separability

 

딥 뉴럴 네트워크의 각 레이어는 입력 데이터를 다양한 특성으로 변환하고 중요한 정보를 추출하는 역할을 한다. 이 문장은 이러한 레이어 간의 연결성과 정보 병목 분석 간의 관련성을 강조하며, 정보 병목 분석을 통해 네트워크의 최적 구성을 파악하고 설명하는 것이 가능할 수 있다고 제안하고 있다.