운동하는 공대생
[Deep Learning] GNN - Graph Neural Networks(미완) 본문
1. Background Theories
1.1 Graph representation learning
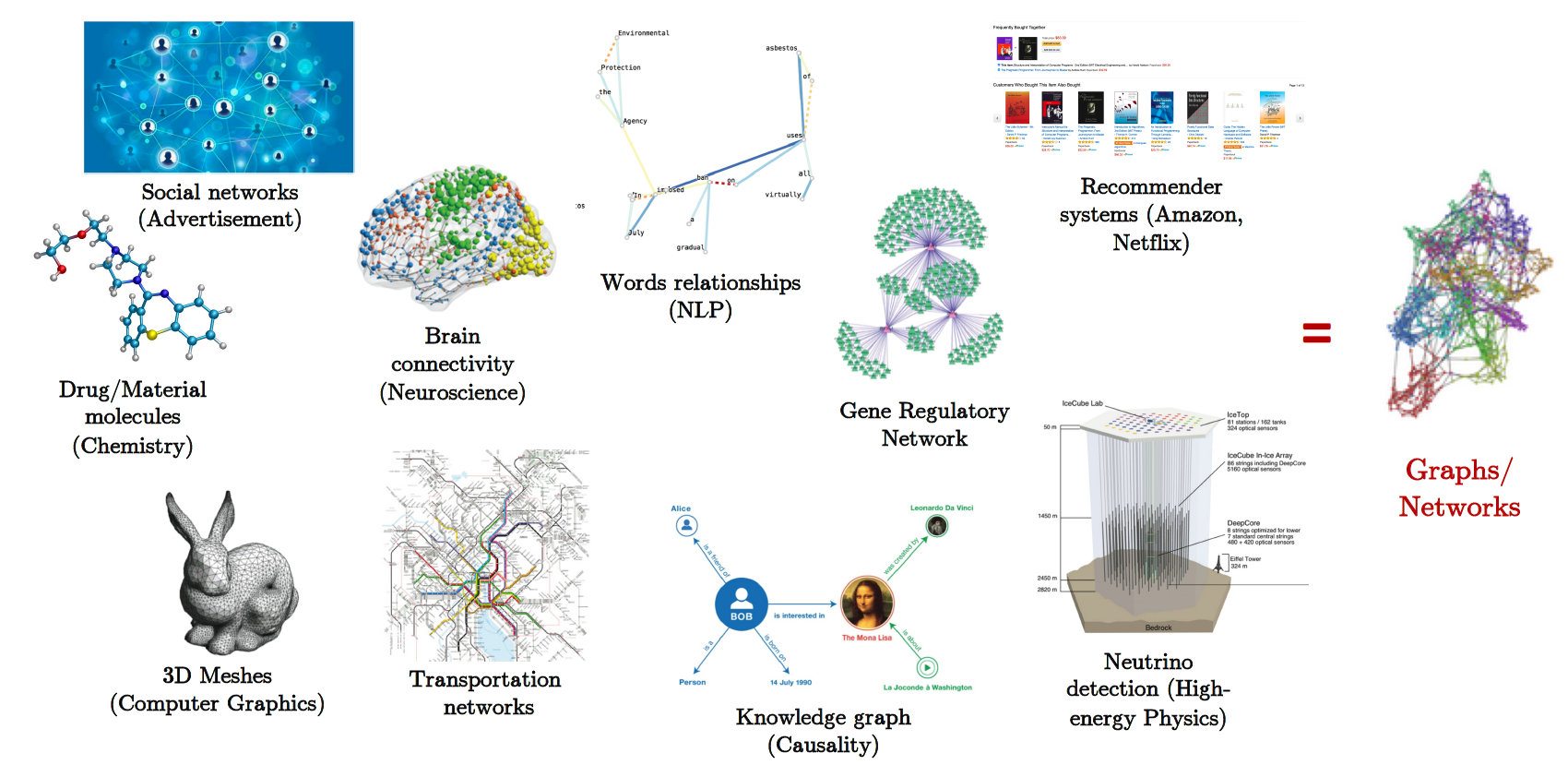
GNN 은 우리가 일상적으로 접하는 데이터중에서 데이터 간의 복잡한 관계를 표현하기에 위해서 등장한 이론이다. 예를 들어 소셜 네트워크, 웹 페이지 및 분자 구조 등이 그래프로 표현될 수 있다. GNN은 이러한 그래프 데이터를 분석하여 패턴, 상호 관계 및 특성을 발견하는 데 사용된다. 모델은 데이터 간의 관계를 이해하고 활용하는 데 사용되며 데이터 간의 상호작용까지도 그룹화가 가능해진다.
1.2 What is a graph?
GNN에서 설명하는 그래프의 구조랑 노드(node)와 간선(edge)을 관계도를 말하는 자료구조를 말한다.

논문에서는 그래프를 G 그리고 그 안에 노드를 V 그리고 간선을 E라고 표현하면 이것을 인접행렬(adjacency matrix)로 표현하는 것인데 이것은 나중에 추가로 설명을 하겠다.
1.3 Node Embedding
그렇다면 이제 그래프 데이터를 어떻게 분석하고 학습을 시키는 데이터로 전환하는 Node Embedding방식에 대하여 이야기를 하겠다.
GNN의 기본적인 임베딩의 목적은 그래프 데이터를 저차원의 임베딩 공간으로 변환하여서 그래프 간의 관계를 표시를 하면서도 그래프 데이터끼리의 관계도 표시한느게 최종적인 목적이다.


위의 사진과 같이 임베딩을 취하는 과정을 '임베딩' 혹은 '인코더'라고도 한다. 임베딩의 최종 목적은 임베딩 과정을 통해서 원래의 기존 그래프 데이터에서의 유사도나 관계를 임베딩 공간에서의 행렬곱으로 표현이 가능하게 하는 것이다. 추가로 이후에 임베딩을 취하고 학습을 진행하고 직접적인 원래 데이터에서의 데이터 간 관계를 알기 위해서는 '디코드' 과정을 거쳐 계산하게 된다.
1.3.1 Shallow Embedding

임베딩 기법중에서 현재는 잘 사용하지는 않지만 가장 기초적인 방식은 'Shallow' 임베딩 방식이다 이 방식은 인코딩 즉 임베딩을 v 노드에 진행을 하게 된다면 indicator vector v와 임베딩 메트릭스 Z의 곱이라고 말할 수 있다.
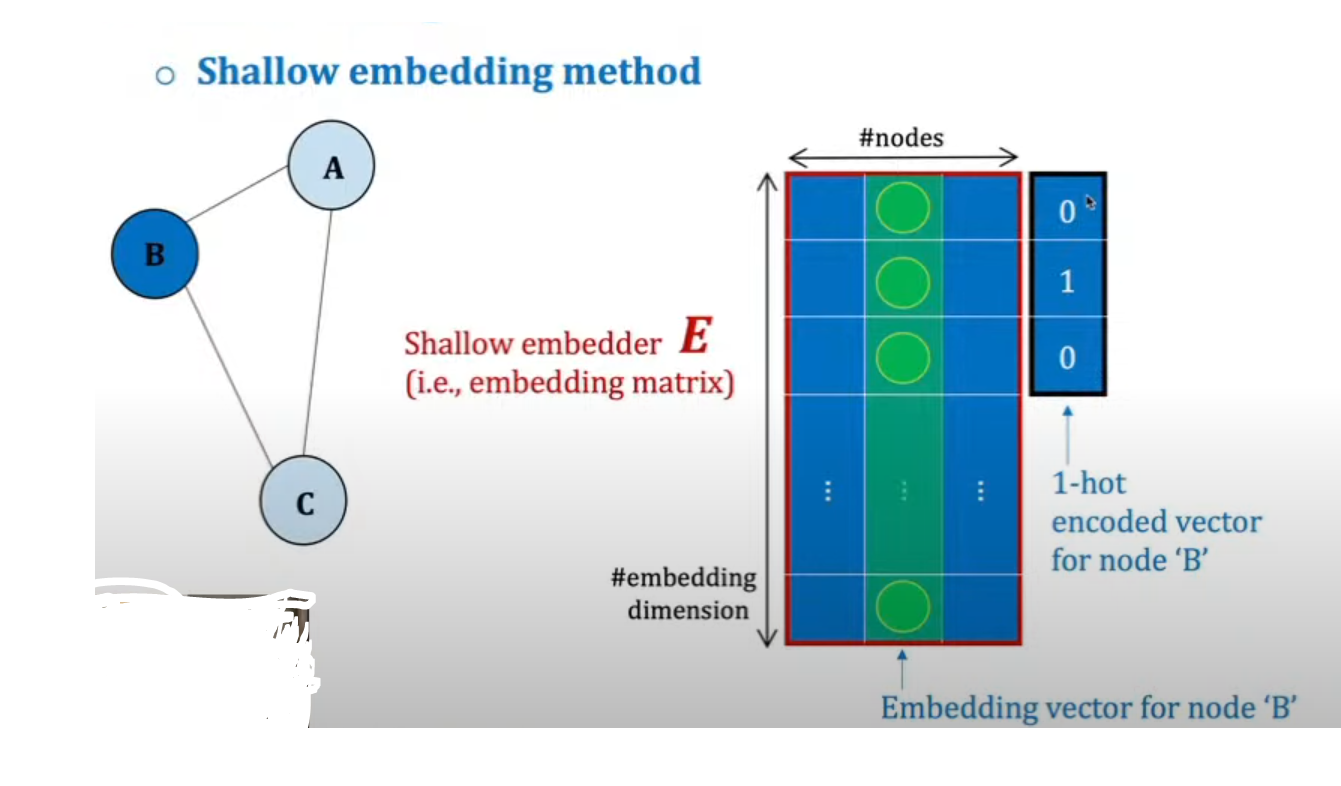
위의 사진과 같이 3개의 노드가 있다고 가정했을 때 B 노드에 대하여 임베딩을 진행한다면 임베딩 matrix(Z)에서 원핫 인코딩을 진행한 indicator vecotr(v)의 곱을 통해서 임베딩 벡터인 초록색 부분이 추출이 된다.
이 임베딩 방식은 unsupervised 한 임베딩 방식으로 하지만 task independent하다.
1.3.2 Random Walk Embedding
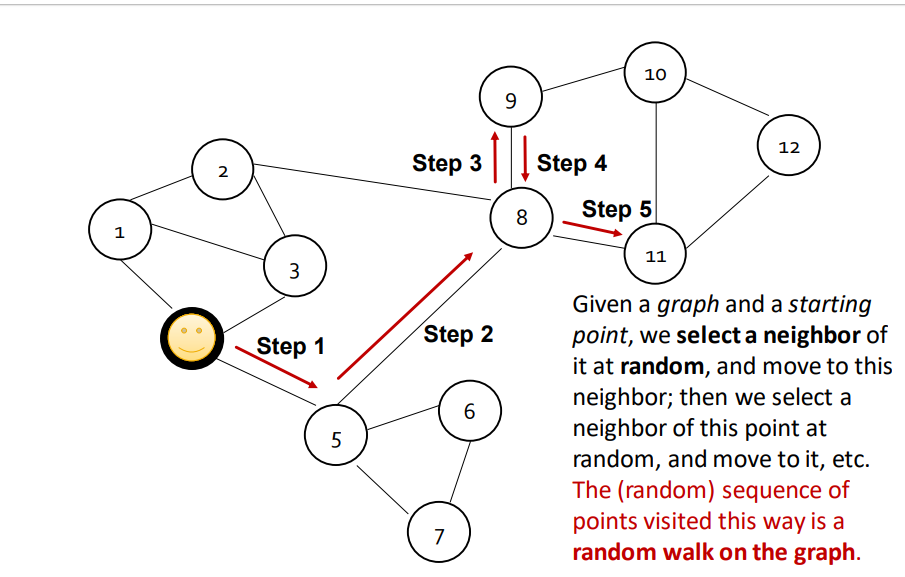
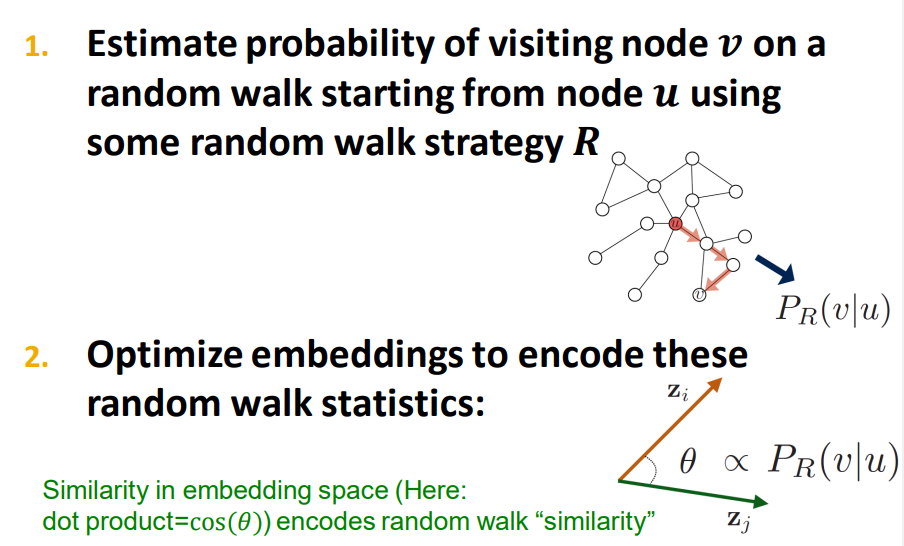
다음 임베딩 방식은 먼저 4번 노드에서 시작을 한다 하면 그래프에서 근처 이웃 노드를 랜덤 하게 선택하고 이동하면서 다음 노드로 넘어간다. 그렇게 이동을 하면서 노드 간 시작 지점과 목적지의 probability를 예측하며 두 노드 사이의 관계를 거리에 따라 probability로 계산하는 방식이다. 최종 목적으로는 비슷한 거리에 있는 노드들은 임베딩 과정을 거치면서도 유사성(거리)을 유지하며 임베딩된다.
그러면 이제 Random Walk의 작동 방식에 대하여 설명하겠다.
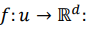
=> 임베딩의 목표로 그래프에서 한 노드 u에서 임베딩 차원의 R에서의 어떻게 매핑을 시키는지 즉 임베딩을 어떻게 할 것인지가 목표이다.
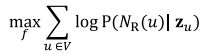
=> 위의 식과 같이 임베딩이 진행이 됩니다. 이것은 인접 노드 간의 Random work N(u)와 u 노드의 임베딩값 zu의 확률의 합이 최대가 되도록 하는 값이 여야 한다.
더 자세하게 설명을 하자면

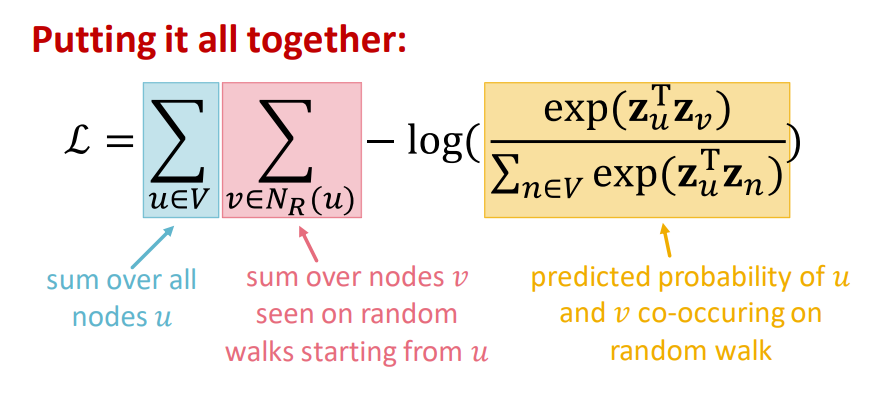
요약하면, Random walk embedding을 생성하기 위한 단계는 다음과 같다
1. 그래프의 각 노드 u에서 시작하여 일정한 길이의 무작위 이동을 실행한다. 이 무작위 이동은 특정한 무작위 이동 전략 R에 따라 수행된다.
2. 각 노드 u에서 시작한 무작위 이동을 통해 방문한 노드들의 다중 집합 NR(u)를 수집한다. NR(u)는 노드 u에서 시작한 무작위 이동에서 방문한 노드들의 집합이다.
3. 임베딩을 최적화하기 위해 다음을 수행한다: 주어진 노드 u에 대해, 노드 u의 이웃 노드 NR(u)를 예측한다.
오른쪽 그림은 전체 식인데 먼저 전체의 노드 u를 합으로 구성되고 그 안에는 u에서 시작되는 random walk에서 노드의 합으로 이루어지고 또한 이후에는 co-occur 즉 같은 노드를 방문하는 경우의 환율을 제외한 환율이다. 하지막 복잡도가 아주 높다.
'Deep Learning > NLP' 카테고리의 다른 글
| [NLP] 워드 임베딩(Word Embedding 2/2)- 예측 기반 벡터(Word Embedding, Word2Vec) (0) | 2022.12.28 |
|---|---|
| [NLP] 워드 임베딩(Word Embedding 1/2)-BOW,Count Vector (0) | 2022.12.28 |
| [NLP] 워드 임베딩(Word Embedding 1/2) - TF-IDF(Term Frequency - Inverse Document Frequency) (0) | 2022.12.01 |
| [NLP] 레벤슈타인 거리(Levenshtein Distance) (0) | 2022.11.17 |
| [NLP] 텍스트 분석이란? (0) | 2022.11.16 |



