[NLP] 레벤슈타인 거리(Levenshtein Distance)

What is Levenshtein Distance

---

 레벤슈타인 거리는 문자열의 유사도를 판별하는 알고리즘의 한 방식으로 두 문자열 사이에 같아지기 위한 연산을 최소화하는 값을 찾는 알고리즘이다. 여기서 연산이랑 수정, 삭제, 삽입 이렇게 3가지 연산을 칭한다.

 

출처: https://jino-dev-diary.tistory.com/entry/Algorithm-%EB%AC%B8%EC%9E%A5%EC%9D%98-%EC%9C%A0%EC%82%AC%EB%8F%84-%EB%B6%84%EC%84%9D-%ED%8E%B8%EC%A7%91-%EA%B1%B0%EB%A6%AC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Levenshtein-Distance

위의 사진처럼 1차 수정에서 4번 삭제에서 1번 삽입에서 1번 총 6번의 비용이 필요한 문자열이다. 

 

Levenshtein Distance Process

---

 레벤 슈타인은 그렇다면 어떤 방식으로 작동하는지 알아보겠다. 기본적으로 LCS 알고리즘과 유사하게 알고리즘이 작동한다. 

 

LCS

• LCS: 최장 공통 부분수열 문제는 LCS라고도 불린다. 이는 주어진 여러 개의 수열 모두의 부분수열이 되는 수열들 중에 가장 긴 것을 찾는 문제다

 

사전적인 의미는 이렇지만 이해를 위해서 사진으로 설명을 더 하겠다.

 

 

 

 

 

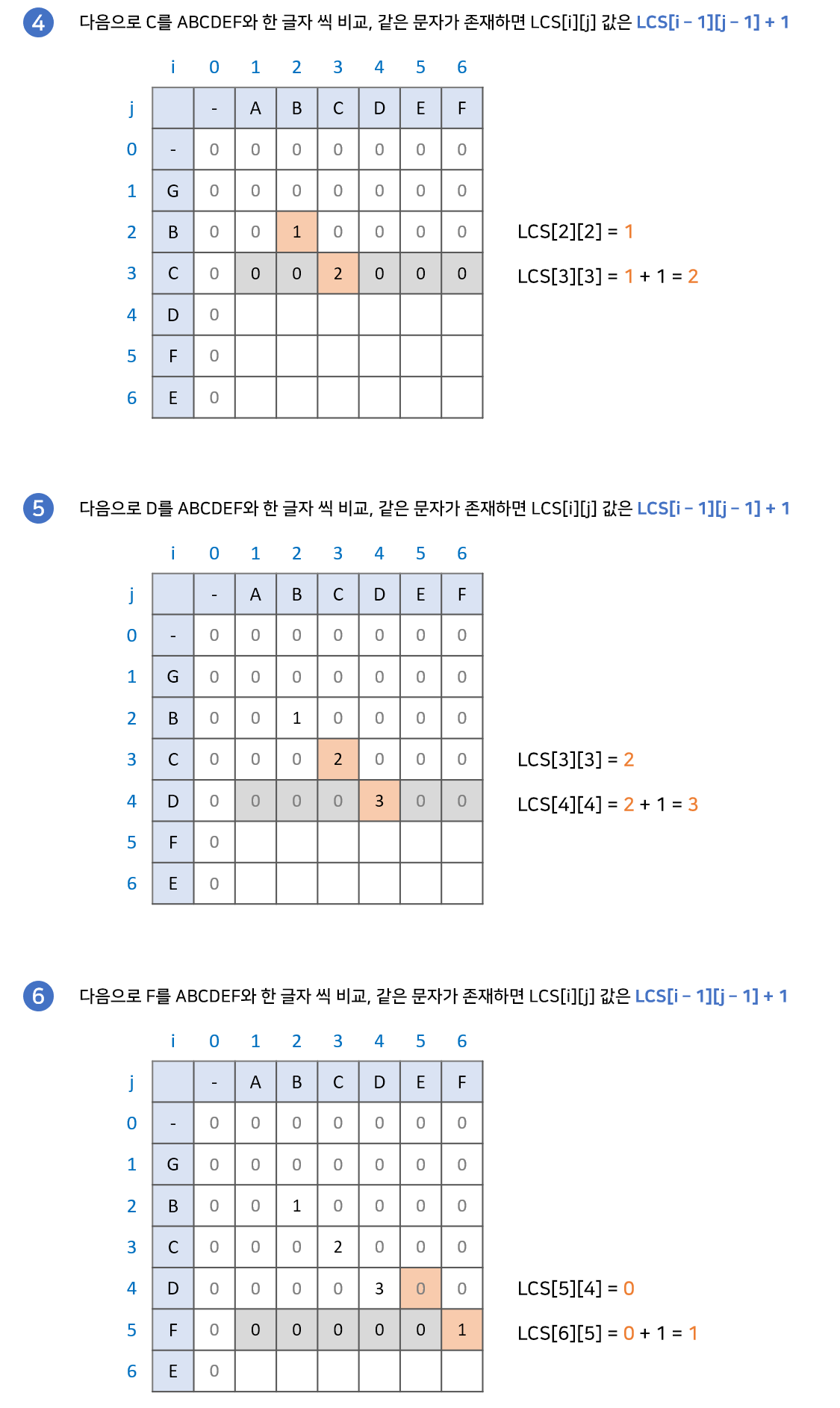
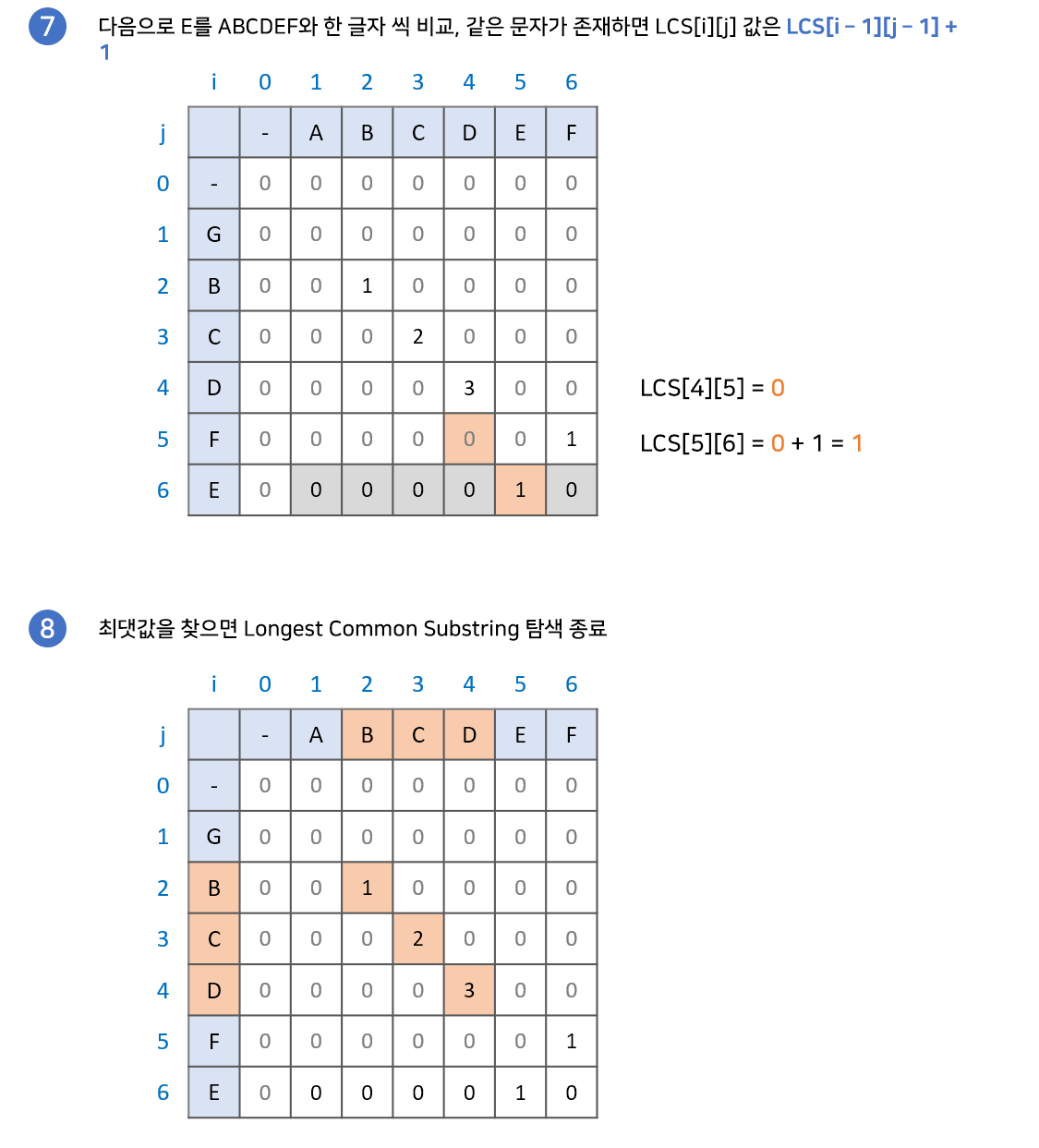
Levenshtein Distance

그렇다면 Levenshtein Distance에서는 어떻게 이 알고리즘이 적용되는지 설명을 해보겠다. 

출처: http://ntz-develop.blogspot.com/2011/03/fuzzy-string-search.html

 

 

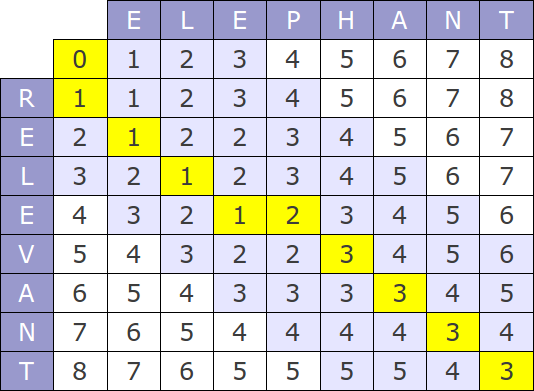
• 글자가 서로 동일하면 대각선 값을 가져온다
• 변경이 필요하면 대각선 값에서 + 1을 한다.
• 삽입이 필요하면 위의 값에서 +1을 한다.
• 삭제가 필요하면 왼쪽 값에서 +1을 한다.
• 최종 값(최솟값)을 반환한다.

 

 

 

 

 

 

code

 

function LevenshteinDistance(char s[0..m-1], char t[0..n-1]):
    // create two work vectors of integer distances
    declare int v0[n + 1]
    declare int v1[n + 1]

    // initialize v0 (the previous row of distances)
    // this row is A[0][i]: edit distance from an empty s to t;
    // that distance is the number of characters to append to  s to make t.
    for i from 0 to n:
        v0[i] = i

    for i from 0 to m - 1:
        // calculate v1 (current row distances) from the previous row v0

        // first element of v1 is A[i + 1][0]
        //   edit distance is delete (i + 1) chars from s to match empty t
        v1[0] = i + 1

        // use formula to fill in the rest of the row
        for j from 0 to n - 1:
            // calculating costs for A[i + 1][j + 1]
            deletionCost := v0[j + 1] + 1
            insertionCost := v1[j] + 1
            if s[i] = t[j]:
                substitutionCost := v0[j]
            else:
                substitutionCost := v0[j] + 1

            v1[j + 1] := minimum(deletionCost, insertionCost, substitutionCost)

        // copy v1 (current row) to v0 (previous row) for next iteration
        // since data in v1 is always invalidated, a swap without copy could be more efficient
        swap v0 with v1
    // after the last swap, the results of v1 are now in v0
    return v0[n]