운동하는 공대생
[수업] 패턴인식 - Supervised learning(4&5) 본문
1. Linear Basis Function Models
이전까지는 모델에 대하여 단지 다항함수로만 표현을 했지만 이것을 통합적으로 표현 가능한 수식이 존재한다.

여기서 parameter값이 w를 제외한 함수를 basis 함수라고 이야기한다. 다항함수로 구성된 basis 함수를 M 값에 따라서 다양하게 표현이 가능하고 이는 matrix의 형식으로 표현한다.


기본 식에서 basis function 이 이제 일반적인 다항함수 일 때의 모습을 왼쪽 그림으로 표현이 가능하다. 가우시안을 따르는 basis function은 uj의 값에 따라서 위치만 이동할 뿐 모양을 일정하다. 하지만 uj와 s는 각각 하이퍼 파라미터로서 가각 위치와 스케일을 지정한다.
이렇게 값을 구분하는 basis function 을 지정하는 방식이 여러 개 있다는 걸 알았다면 이런 weight parameter를 학습하기 위해서는 기존에 이야기했었던 LSM(Least Square Method) 방식이나 MLE(Maximum Likelihood Estimation) 방식을 사용한다.
2. MLE(Maximum Likelihood Estimation)
2.1 Bayesian rule

MLE 가 Bayesian rule 을 따른다. 이는 식으로 본다면 데이터 D 모집단에서 θ 가 일어날 확률은 구한다고 했을 때, tlrdms likelihood와 prior의 값을 evidence로 나누어 이 값을 구합니다.
실질적으로 전체 데이터에서의 D 데이터의 확률과, 다른 모든 파라미터의 확률중 θ 에 대한 확율인 prior 값을 구하기란 쉽지 않다 그래서 이는 likelihood값을 최대로 하도록 하는 확률을 찾는다면 p(θ | D) 값의 최대를 찾는 것이 가능하다.
2.2 MLE
이것이 MLE이론의 시작저므올 데이터에서 파라미터값이 최대가 되도록 하는 θ 값을 likelihood 값을 통해서 찾아나간다.

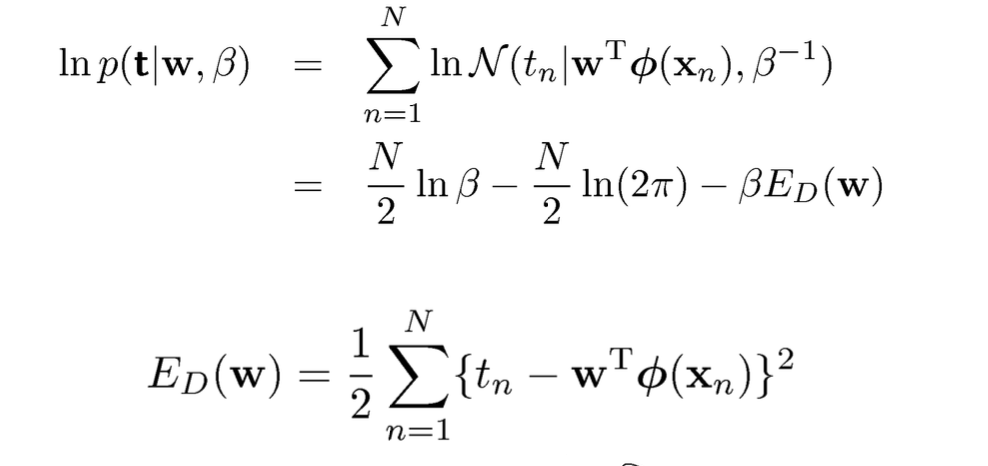
MLE에서 중요한 방식은 일단 구하는 target데이터에 대하여 noise가 포함된 확률값들을 데이터의 수만큼 곱한다. 그 이후에는 계산을 위해 양쪽에 로그를 씌워서 값을 진행하다 보면 ED(w) 이 값이 남게 된다. 그래서 확률값을 최대로 하기 위해서는 ED(w) 값이 최소가 되어야한다. 그래서 이것을 target 값에서 예측값을 빼고 제곱한 값을 모두 더하는 LSE (Least Square Method) 방식과도 같아지는 모습을 보인다.
'수업' 카테고리의 다른 글
| [수업] 기계학습 - Linear Regression (2) (0) | 2023.10.08 |
|---|---|
| [수업] 기계학습 - Linear Regression (1) (0) | 2023.10.07 |
| [수업]패턴인식 - Supervised learning(7) (0) | 2023.09.30 |
| [수업] 패턴인식 - Supervised learning(3) (0) | 2023.09.29 |
| [수업] 패턴인식 - Supervised learning(2) (0) | 2023.09.29 |




