운동하는 공대생
[수업] 패턴인식 - Supervised learning(3) 본문
이전까지 이제 Error를 구하는 함수 objective function과 그리고 그 함수를 최소화하는 gradient descent 방식에 대하여 알아보았다.
1. Polynomial curve fitting


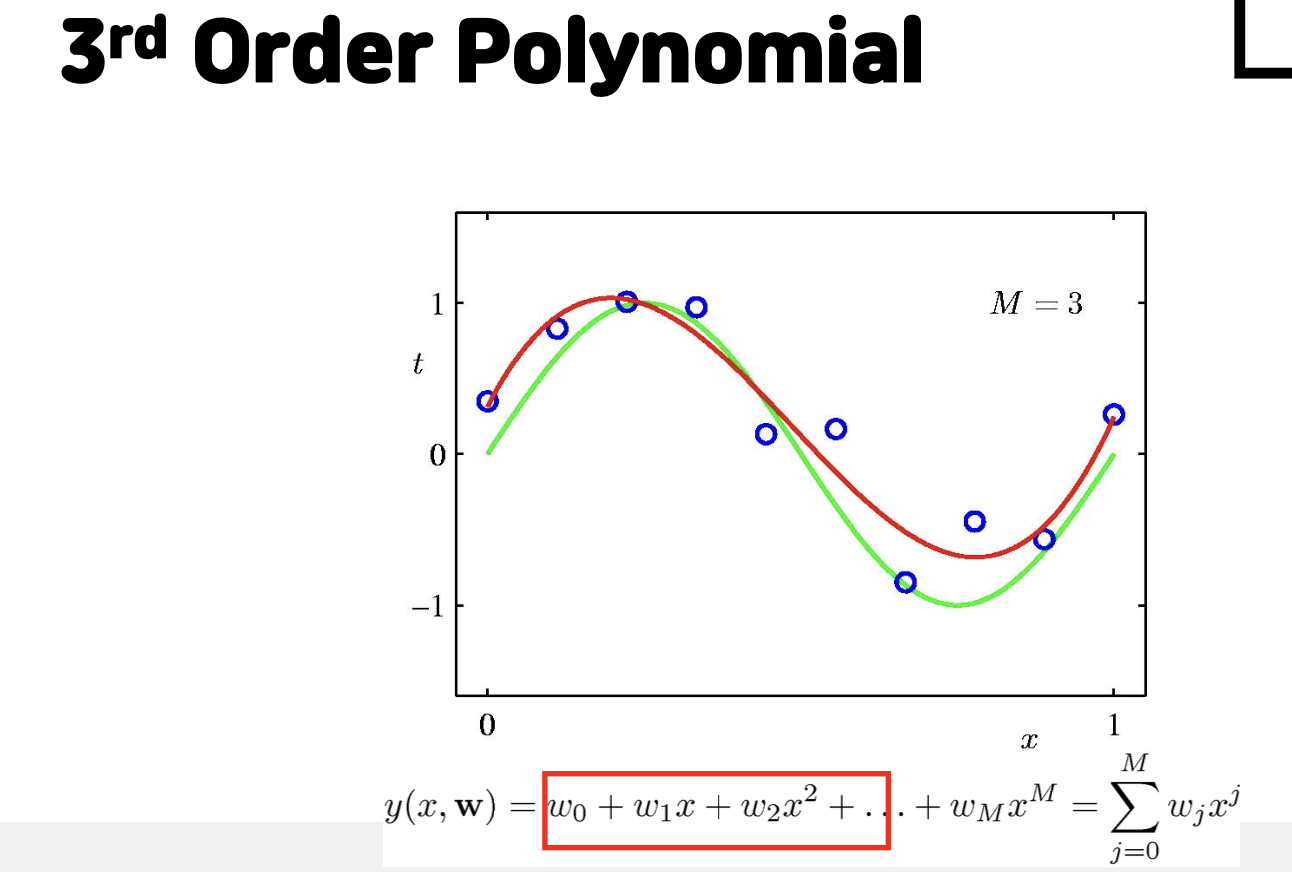
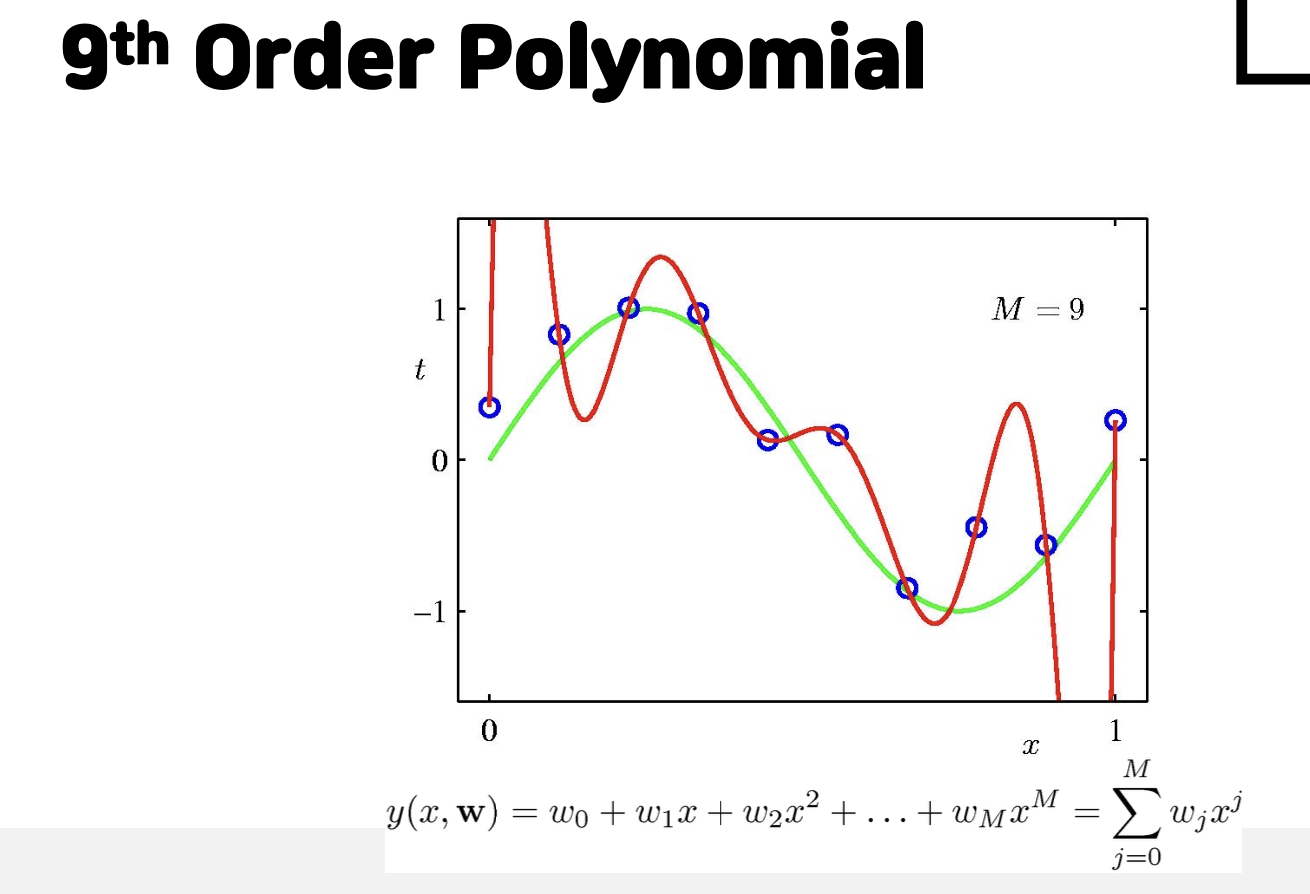
위의 그림처럼 각 예측하는 함수를 구성할때 다항함수를 이용할 때 차수를 늘리면 발생하는 문제들을 볼 수 있다. 차수가 너무 낮아 모델이 단순하면 첫 번째 그림처럼 모들 데이터들을 구분하기가 어렵다. 그리고 너무 차수가 높으면 과적합 문제인 overfitting이 발생한다.
2. Overfitting , Unterfitting
이제 2가지 가정을 하고 예시를 통해서 이해를 해보자.
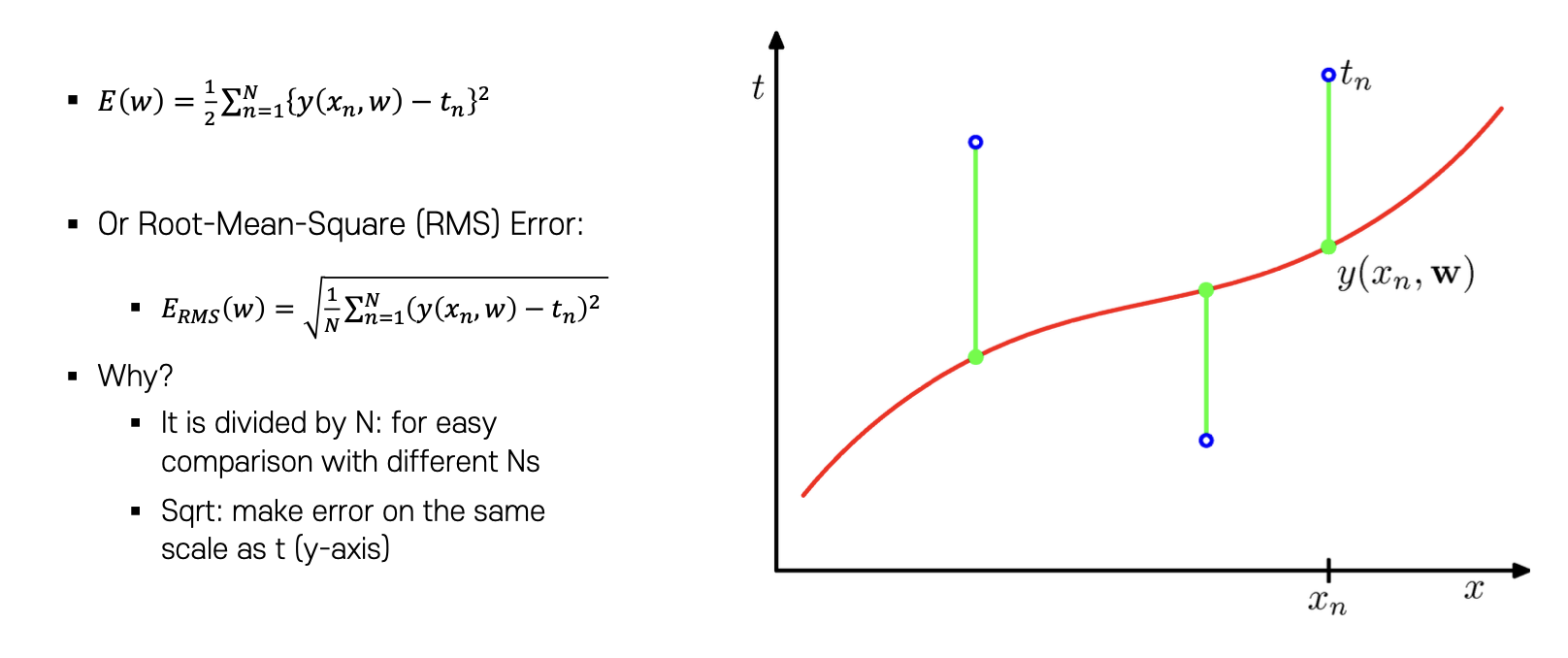
가정 1: 먼저 Error를 계산하는 함수는 RMS(Root-Mean-Square) Error 함수로 지정한다. 이는 데이터 포인트와 Regression 모델 function 간의 차이를 계산하는 방식이다.
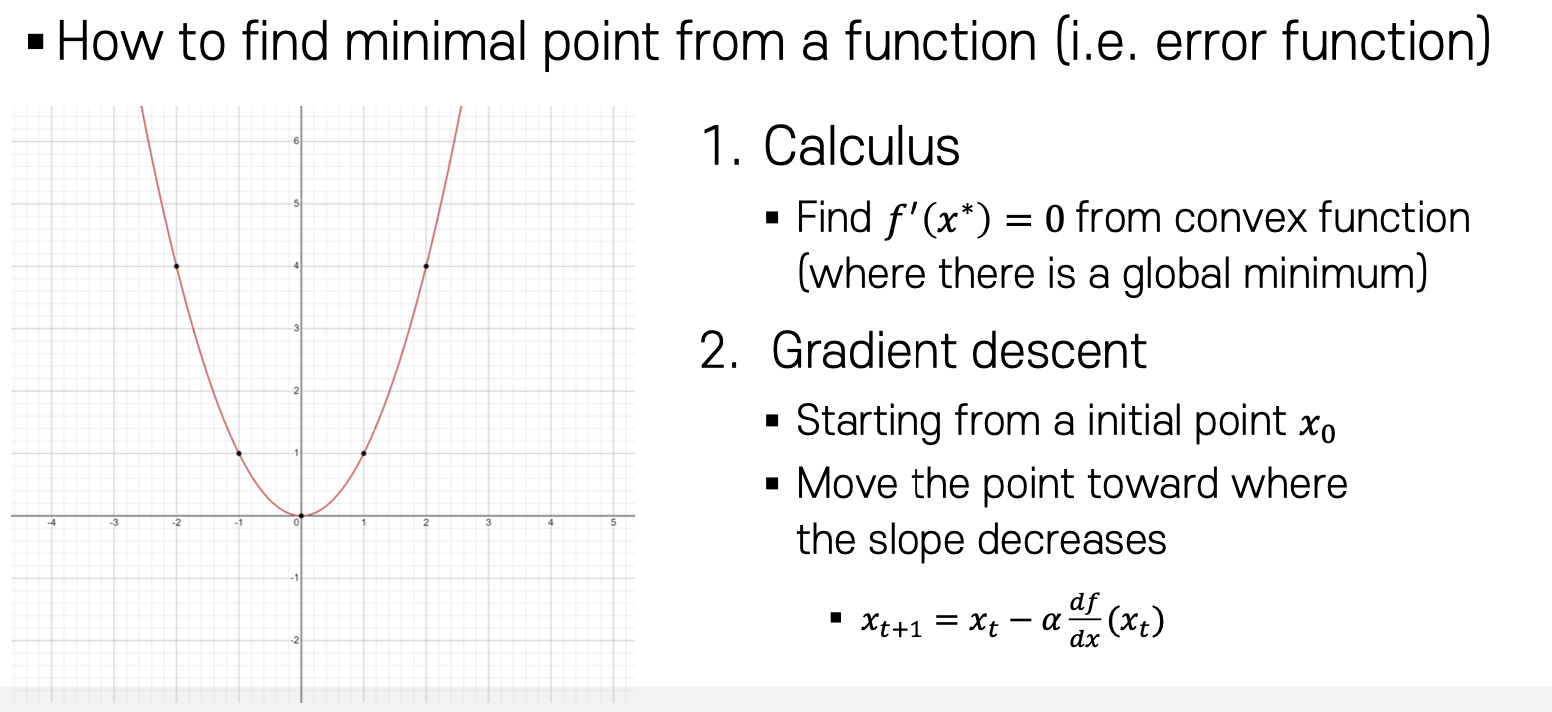
가정 2: 이후에는 Error를 최소화 하기위해서 미분값이 0 이 되는 지점(convex)을 찾거나 혹은 임의의 지점에서 시작하여 값을 찾아 나가는 Gradient descent 방식을 사용한다.
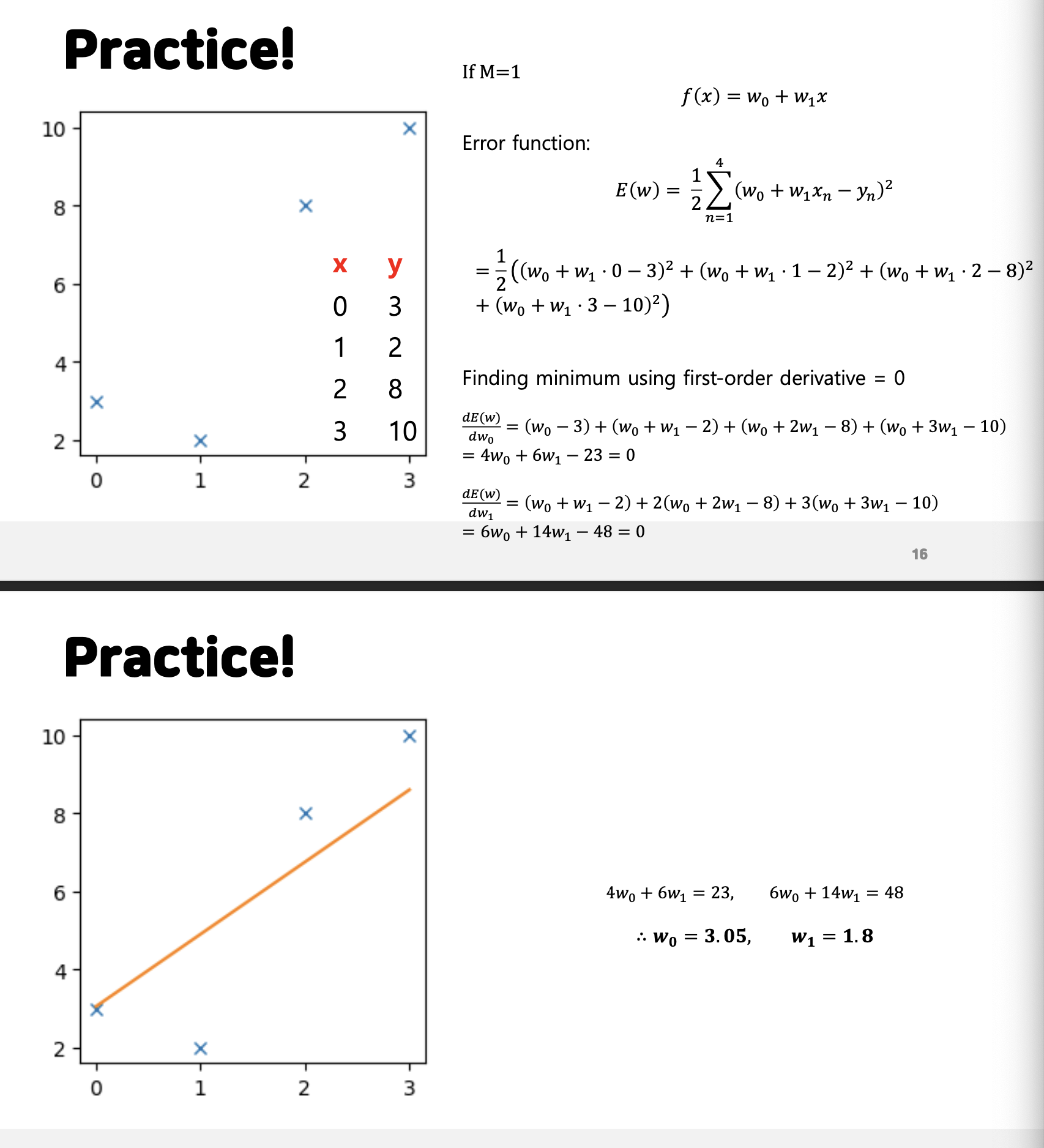

위의 두 방식처럼 다항함수의 차수가 1이거나 3 인 경우에 대한 parameter를 error 함수로 구하는 방식을 보인다. 하지만 여기서 구하는 방식이 차수가 늘어감에 있어서 상당히 복잡해지는 문제가 발생한다. 또한 이전에 설명했던 것처럼 차수가 올라가면 overfitting의 문제가 발생한다.
3. Why is overfitting a Serious Problem?
Overfitting이 심각한 이유는 Test Set 에 대한 Error 때문이라고 말할 수 있다. 보통 모델을 학습함에 있어서 모델에 대한 성능 평가는 모델이 학습하지 않은 데이터를 기준으로 평가를 실시한다. 하지만 과적합의 문제가 발생하면 train set에서는 Error가 발생하지 않아도 새로운 데이터 test set이 들어오면 정확한 예측값을 도출하기 어렵다. 그래서 관접합 문제는 훈련과정에서 보다는 그 모델이 실질적으로 사용되는 상황에서 심각한 문제를 야기한다.
이를 해결하기 위해서는 데이터를 늘리거나 Regularization 하는 방식이 있다. 단순히 데이터를 늘리게 된다면 모델이 분류하는 분류 기준들이 복잡하더라도 많은 데이터를 분류하기에 적합한 모델이 될 수 있다.
- Regularization
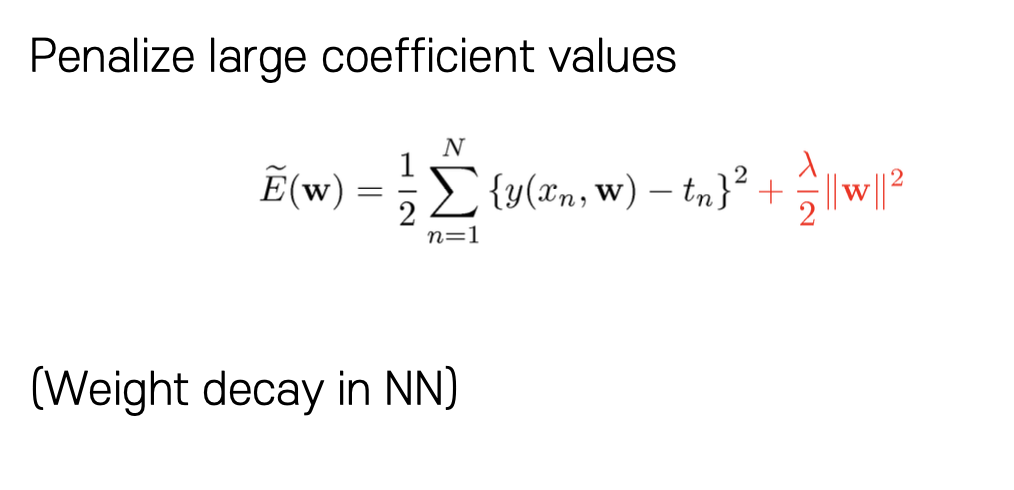
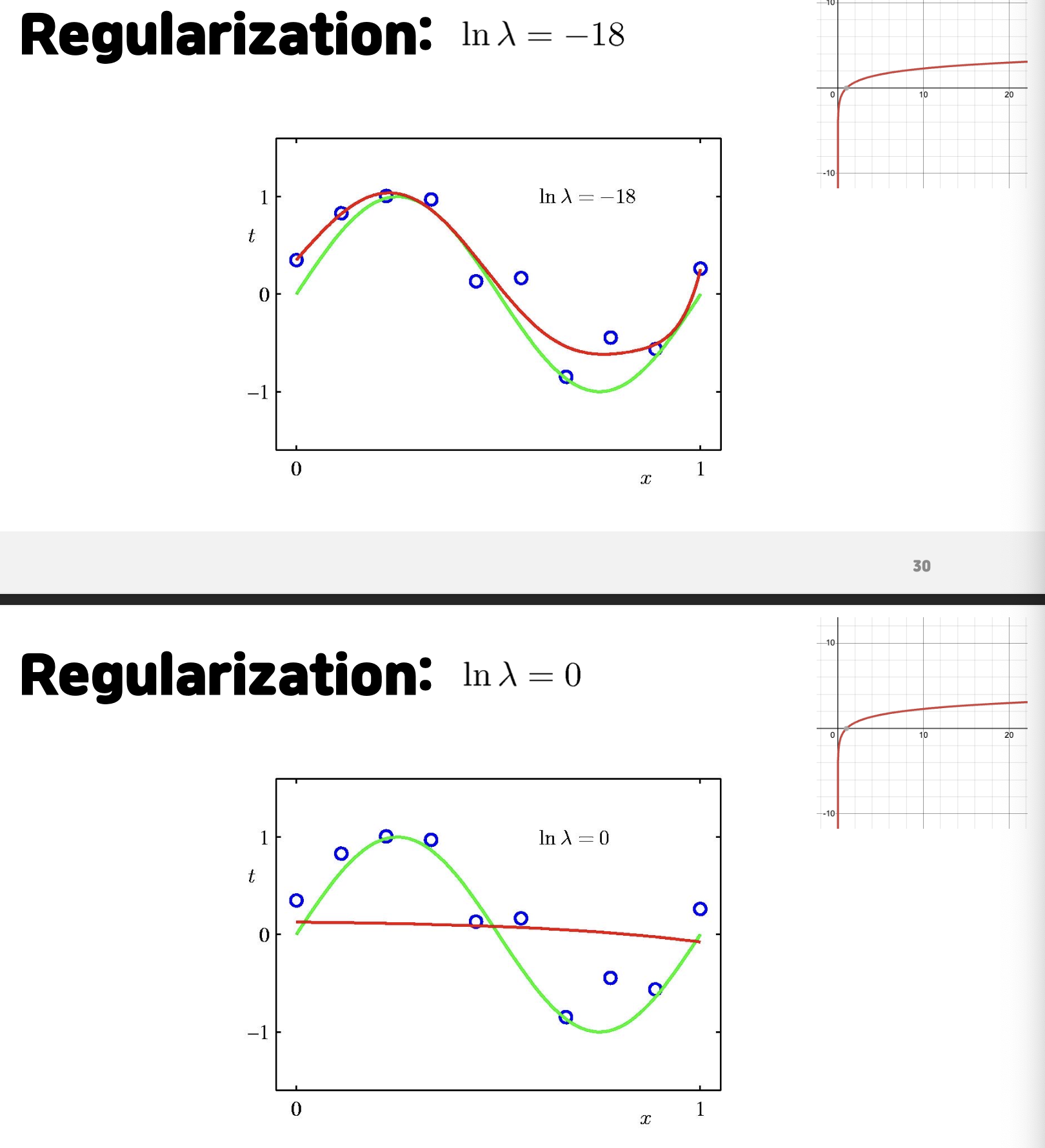
Error function 에서 뒤에 regularization 하는 값을 추가로 하여 Error를 구하는 과정에서 값이 너무 커지거나 작아지는 문제를 해결하여서 과적합 문제를 조금 해결한다. 이는 함수를 구성하는 과정에서 변화량을 제안하는 효과가 있다. 하지만 이는 너무 값을 크게 한다면 변화가 전혀 일어나지 않아서 오히려 과소적합(Underfitting) 문제가 발생하기도 한다.
'수업' 카테고리의 다른 글
| [수업] 기계학습 - Linear Regression (2) (0) | 2023.10.08 |
|---|---|
| [수업] 기계학습 - Linear Regression (1) (0) | 2023.10.07 |
| [수업]패턴인식 - Supervised learning(7) (0) | 2023.09.30 |
| [수업] 패턴인식 - Supervised learning(4&5) (0) | 2023.09.30 |
| [수업] 패턴인식 - Supervised learning(2) (0) | 2023.09.29 |




