운동하는 공대생
[논문]KAN: Kolmogorov–Arnold Networks 본문
https://arxiv.org/abs/2404.19756v4
KAN: Kolmogorov-Arnold Networks
Inspired by the Kolmogorov-Arnold representation theorem, we propose Kolmogorov-Arnold Networks (KANs) as promising alternatives to Multi-Layer Perceptrons (MLPs). While MLPs have fixed activation functions on nodes ("neurons"), KANs have learnable activat
arxiv.org
1. Introduction
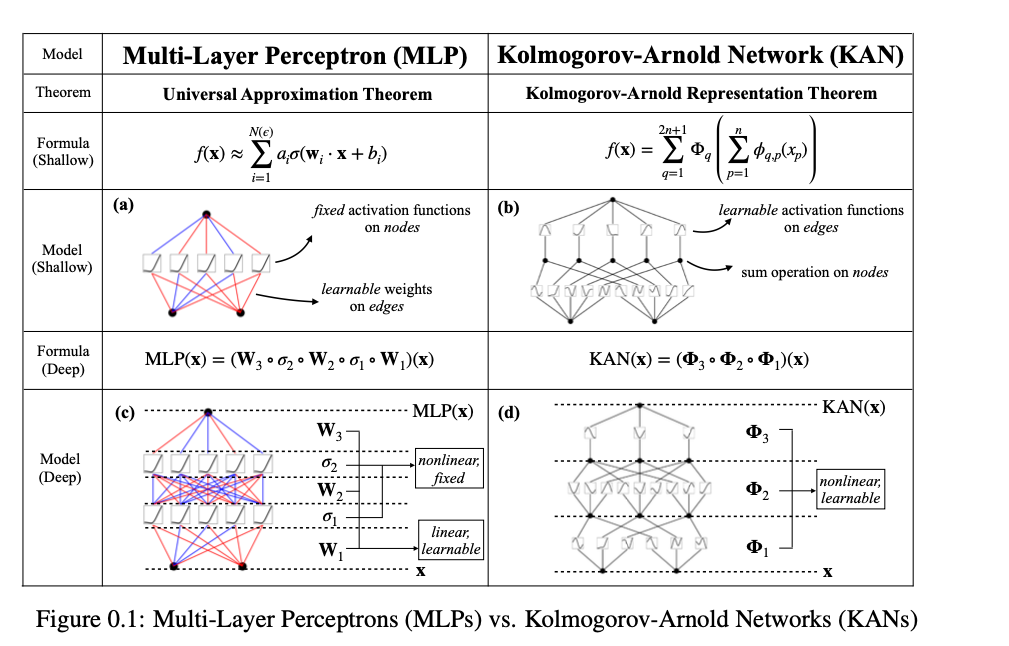
KANs 네트워크 방식은 MLP를 대체하는 새로운 방식의 layer로 본 논문에서는 소개하고 있다. MLPs 같은 경우에는 그 단점이 transformers에서 명확하게 나타나는데 파라미터의 대부분을 Linear layer에서 소모하지만 attention layer보다 성능을 보이진 못한다. KANs 은 일반적인 MLPs 와는 다르게 학습이 가능한 edges로 이루어져 있고 matrix 형식으로 이뤄지게 아니라 1D로 이루어져 있다. KANs의 노드는 MLP보다 더욱 경량화된 구조를 가지고 있다.
Kolmogorov-Arnold 이론을 이용한 연구는 이전부터 활발하게 진행이 되었다. 하지만 깊이 2 너비 2n+1 까지만 연구가 진행이 되었다. 이런 문제를 해결하며 임의의 깊이와 너비를 사용한 일반화된 방식을 KANs 네트워크에 적용했다고 이야기 합니다. KANs 은 Splines와 MLPs의 장점을 그대로 가지면서 단점을 극복을 하였습니다. Splines는 저 차원에 대한 결정에 정확도는 높지만 고차원에 대한 curse of dimensionality(COD)에 대한 문제는 해결하지 못하는 문제가 있다. MLPs 같은 경우에는 COD에 대한 문제는 적지만 적은 차원에 대한 정확도는 조금 낮다.
모델을 학습함에 있어서 구성적 구조의 학습과 단변량 함수 근사를 모두 이루어야 한다.
구성적 구조 학습: 전체 함수를 구성하는 여러 하위 함수들이 어떻게 결합되어 있는지 이해해야 합니다.
단변량 함수 근사: 각 하위 요소 또는 단변량 함수들을 정확히 표현하고 근사해야 합니다.
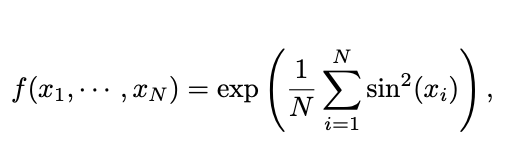
그래서 KANs 은 밖에는 MLPs 를 안에서는 splines을 사용한다. 결과적으로 KANs은 feature에 대한 학습이 이루어질 뿐만 아니라 좋은 성능도 가지고 있다.
2. Kolmogorov-Arnold Networks
2.1 Kolmogorov-Arnold Representation theorem
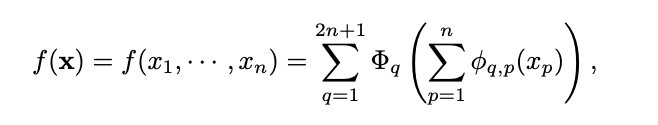
고차원의 연속함수는 단변량 함수들의 합으로 표현이 가능하다고 이야기를 합니다. 즉 이말은 머신러닝에서 다항함수의 1D 함수로 고차원 함수를 학습하는 게 가능하다는 이야기입니다. 하지만 이런 1D 함수는 고르지 않으며 깨지기 쉽습니다. 이론적으로는 좋아 보이지만 실제 적용하면 성능을 보이지 않았습니다.
즉 수식을 보고 다시 이야기를 한다면 외부와 내부의 파이값으로 고차원에 대한 데이터를 단순한 함수들의 결과의 합으로서 표현을 하여 고차원에 함수를 조금 더 단순하게 표현하는게 가능하다.
2.2 KAN architecture
KAN의 구조는 앞서 설명했던 고차원의 함수를 단변량 함수로 나누어 주는 방식인데 여기서 단변량 함수를 찾는것이 주목적이다. 이런 아이디어를 통해서 1D function을 B-spline curve방식을 통해서 단변량 함수를 학습하는 방식을 고안해 냈다. local B-spline 함수에 대한 계수를 학습하는 방식이다.
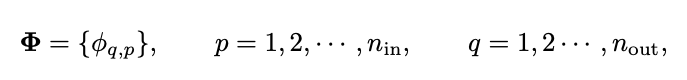
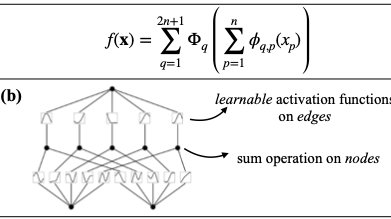
하지만 이런 KAN 방식은 단순하게 그림처러 2 layer로 구성하는 것이 아니라 더 깊고 넓게 구성을 해야 하나. KAN layer를 깊게 쌓기 이전에 먼저 KAN layer 란 무엇인가를 먼저 답을 해야 한다. KAN은 먼저 n차원의 input과 n 차원의 outpu 차원이 있다면 이것을 1D 함수로 정의를 해야 한다.
파이값은 학습이 가능한 파라미터라고 했을 때 쉬의 사진에서 식에서 내부의 함수는 $n_{in} = n$ 과 $n_{out} = 2n+1$ 의 차원을 반환하고 외부의 함수는 $n_{in} = 2n+1$ 와 $n_{out} = 1$ 의 형식으로 Kolmogorov-Arnold를 구성한다. 그래서 KAN의 단순한 2개의 layer는 단순하게 구성이 가능하지만 deep KAN을 한들기 위해선 KAN layer를 단순하게 쌓아 올리면 된다.
전체 구조
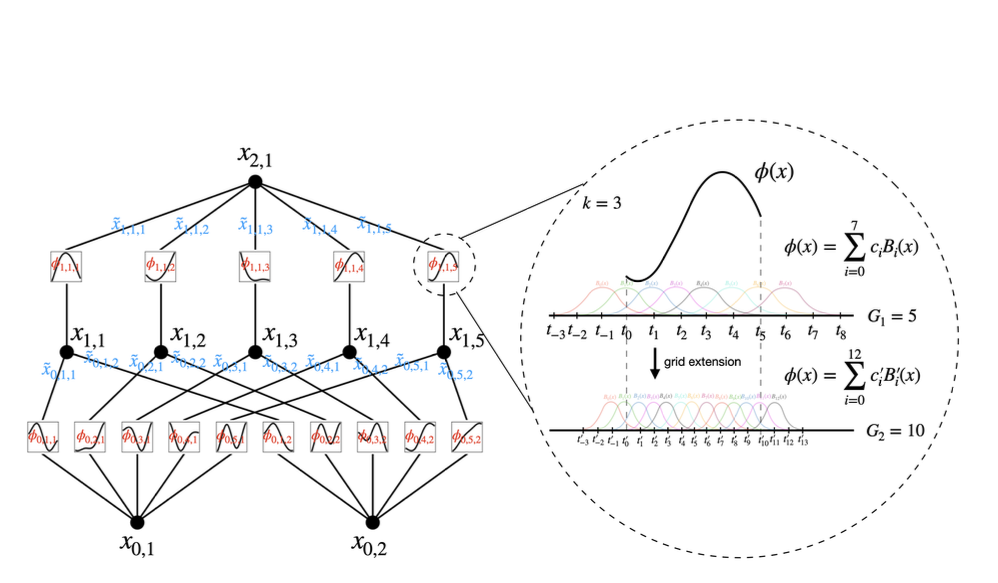
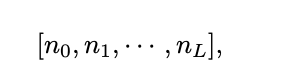
먼저 i 번째 layer에 노드의 개수를 $n_i$라고 표현을 먼저 한다고 했을 때, $l^{th}$ 번째 layer에서 $i^{th}$ 의 뉴런을 (l, i)라고 표현을 한다고 할 때 (l, i) 뉴런의 활성화 값은 &x_{l, i}&라고 표현을 합니다. 또한 $l$ layer와 $l+1$ layer 사이에서 layer는 전부 $n_{l} n_{l+1}$ 개의 활성화 함수를 필요로 합니다. 이런 활성화 함수는 아래의 식과 같이 표현합니다.
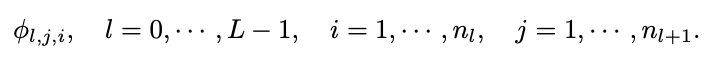
전체 구성의 이미지에서 처럼 activation value $x_{l+1, i}$ 를 결정하기 위해서는 이전 layer에 있는 노드들을 activation 함수를 거친 이후의 $x^~$ 값을 전부 더하여 결정된다 이는 아래의 식에서 확인이 가능하다.
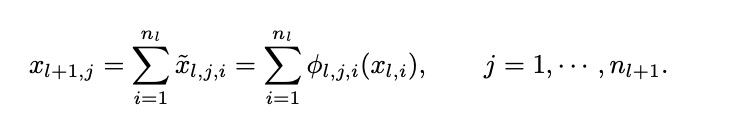
그렇다면 결국 matrix 형식으로 나타내면 아래와 같이 표현이 된다.

$n_L = 1$ 일 때 즉 layer의 노드가 1개 인 상황을 가정하게 된다면 아래와 같은 형식으로 계산이 진행된다.

앞에서 말했던 아래의 Kolmogorov-Arnold 수식에 따르면 2-layer KAN의 형식을 가진다. [n, 2n+1,1]. 또한 모든 연산은 미분이 가능하며 KAN 또한 back propagation이 가능하다.

MLP layer 같은 경우에는 아래의 식과 같이 식이 진행된다. 하지만 여기서 알 수 있듯이 Weight와 activation function의 연산을 KAN에서는 $\Phi$ 하나로 전부 연산이 가능하다.

Implementation details
1) Residual activation function
활성화 함수가 어떻게 구성되는지를 설명을 해보겠다. $\phi(x)$는 basis function $b(x)$ 와 spline 함수들로 이루어져 있다.
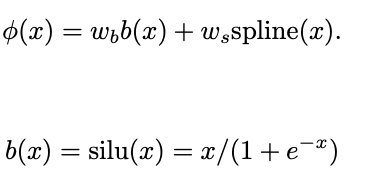
또한 spline(x)는 B-splines 방식으로 여러게의 linear combination으로 표현이 가능하다. 여기서 $c_i$는 학습이 가능한 파라미터가 된다. 그리꼬 또한 w 도 학습 가능한 파라미터로서 작용을 하게 된다.

2) Initialization scales
초기화는 $w_s = 1$ 로 spline(x) 는 0에 가깝게 초기화가 되며 $w_b$ Xavier 초기화 방식을 사용합니다.
Parameter count
1) depth L
2) layers of equal width n0 = n1 = .... nL = N
3) each spline of order K on G intervals
$O(N^2LG)$ 의 파라미터가 KAN layer 에 존재를 합니다. MLP는 $O(N^2L)$ 의 파라미터를 사용합니다. 여기서 단순하게 보면 MLP가 더 적어 보이지만 KAN 방식이 더 적은 width 를 가지고 있기 때문에 더욱 효율적입니다.
