[논문]Learning Sequential Latent Variable Modelsfrom Multimodal Time Series Data

1. Intro 

multivariate time series 데이터에 대한 학습을 진행하는 대표적인 방식인 spatial-temporal graph neural networks 방식이 있다. 이 방식에서는 그래프 구조를 input으로 하여 모델을 학습을 진행한다. 그래프로 구성하지 않는 방식보다 많은 개선점이 있지만 여전히 몇 가지 문제는 남아있다.

 

문제 1 : 대부분의 multivartiate time series 데이터들은 그래프 구조를 하고 있지 않다. 변수들 간의 관계는 데이터를 보고 발견된다.

문제 2: 그래프 구조가 가능하더라고 대부분의 message passing에 주의를 기울이기 때문에 훈련 과정에서 그래프 구조가 optimal 하지 않을 수 있다. 

 

본 논문에서는 이런 문제들을 해결하려고 했다.

sparse graph adjacency matrix 를 그래프 구조로 추출하고 convolution에서는 데이터의 변수들 간의 특징을 추출하였으며, temporal에서는 temporal 패턴을 추출하여 진행하는 구조를 가짐으로 문제 1을 해결하려고 하였다. 그리고 모든 layer는 gradient descent 방식으로 학습이 진행되며 multivariate time series 데이터를 학습하는 동시에 internalgks  그래프 구조도 동시에 진행한다. 그래서 본 논문에서는 "small and large graphs, short and long time series, with and without externally defined graph structures" 한 방식으로 장점이 있다고 말한다.

 

2 Backgrounds

2.1 Multivariate Time Series Forecasting

multivariate time series 예측에서 보통 linear 한 방식으로는 autoregressive integrated moving average(ARIMA), vector auto-regressive model (VAR), Gaussian process (GP) 등등 다양하게 존재하지만 non-linearity 까지 포착하는 딥러닝 기반 모델이 더욱 효과적이다.  CNN 기반 모델은 변수들 간의 관계를 encapsulate 하는 게 가능하지만 잠재적인 dependencies를 이용하는 건 불가능하다. 

 

2.2 Graph Neural Networks

그래프 구조의 네트워크는 거리가있는 엔티티들 간의 관계성을 표현하기에 적합하며 이웃 노드들에게 정보를 전달한다. 따라서 multivariate time series 데이터에서 spatialtemporal graph neural networks는 변수 들까의 관계성을 표현하기에 적합하다. 이 방식은 그래프 구조를 사용하지 않을 때 보다 효과적이지만 원래의 multivariate time series 데이터를 효과적으로 사용하지 못하고 미리 정의된 그래프가 아니거나 생성하는 방식이 부족할 수 있다.

 

3  Framework of MTGNN

3.1 Model Architecture 

모델의 구조는 graph learning layer, m graph convolution modules, m temporal convolution modules, output module 이렇게 구성되어있다.  graph learning layer 는 그래프 구조의 데이터를 학습할 때 adjacency matrix에 대한 값들이 존재하여 노드 간의 관계를 수치화하였고 이후에 Graph Convolution 레이어의 input으로 사용된다. Grap Convolution 레이어는 spatial and temporal dependencies respectively를 포착하는 데 사용된다. Temporal convolution modules 은 아래의 사진처럼 데이터를 변환하는데 사용된다. 여기서 모델의 구조가 깊어지면서 발생하는 gradient vanishing 를 피하기 위해서 residual connections을 추가하여 해결하였고 다음 temporal convolution 모듈의 input으로 Graph covolution 모듈의 output과 추가하여 다음으로 전달된다. 

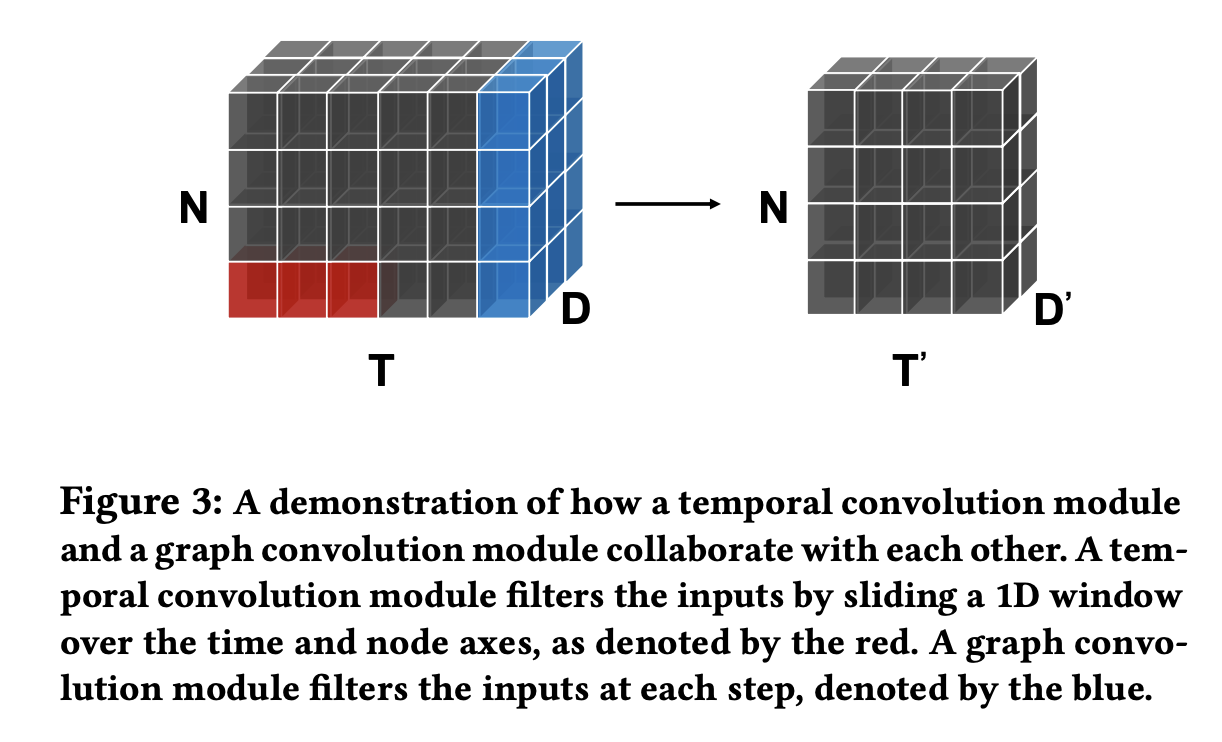
3.2 Graph Learning Layer

3.3 Graph Convolution Module

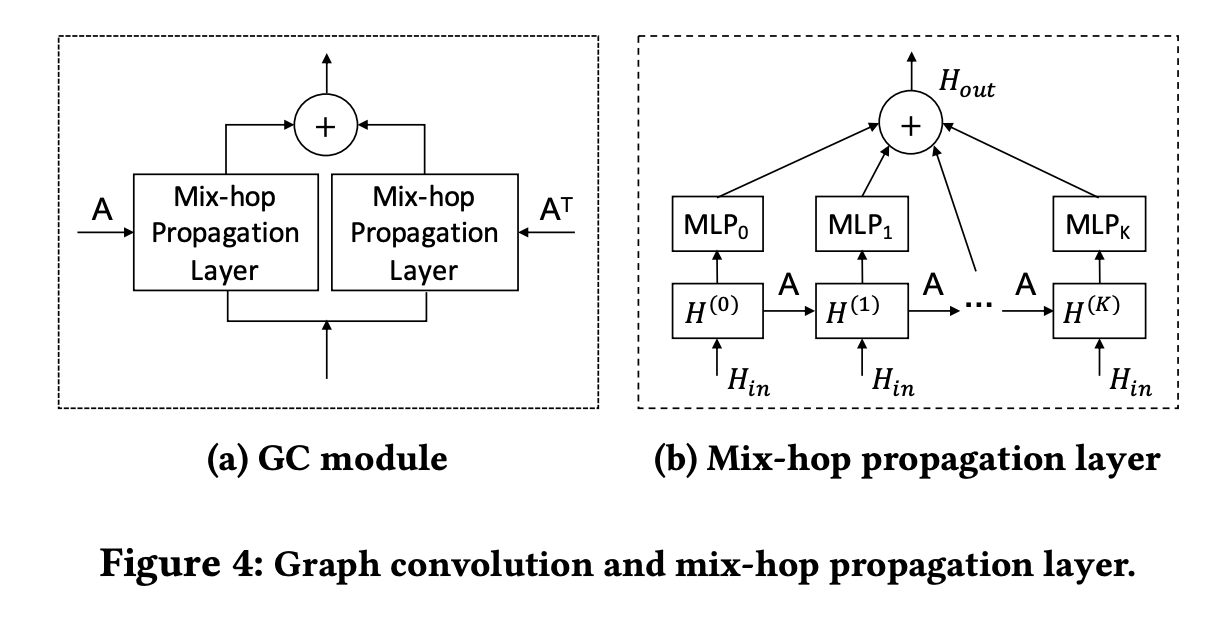
Graph Convolution Module 은 이웃 노드들 간의 정보들을 그래프에 포함시키기 위해서 사용하는 방법으로 2개의 Mix-hop 방식의 합으로 구성된 어이 서다. Mix-hop Propagation Layer는 먼저 GCN 방식을 통해서 한 노드로 정보가 집중되며 그래프의 이웃 노드들 간의 정보들이 추출이 된다. 그래서 여기서는 각 단계의 결과들을 모두 합하여 처리하고 Hout으로 concat 하여 결과를 도출한다.

 

4.4 Temporal Convolution Module

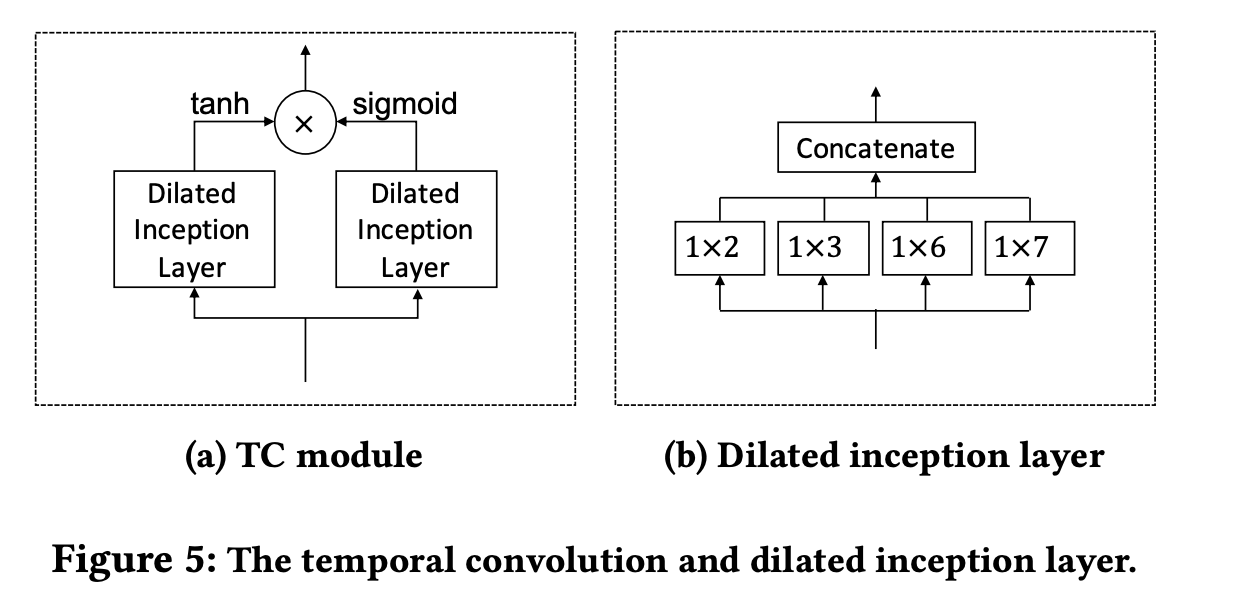
Temporal Convolution 모듈에서는 1D 컨벌루션 필터를 사용하여 시계열 데이터의 순차적인 패턴을 추출하고 이것을 다양한 범위의 시간적 패턴을 발견하고 매우 긴 시퀀스를 처리할 수 있는 시간적 convolution 모듈이다. 그래서 이것을 여러 크기의 필터를 사용함으로서 다양한 정보들을 추출하는 게 가능하다. 그림처럼 여러 가지 필터를 사용하여 결합하고 이것을 2개의 layer로 쌓아서 활용한다. 

 

4.5 Skip Connection Layer & Output Module

skip connection 은 이전의 layer 에서는 시퀀스의 길이에 따라서 다음 모듈의 input으로 값을 넘기는 작업이다. output 모듈은 1*1 크기의 convolution 작업을 통해서 input으로 받은 이전 작업에서의 output을 output의 차원에 맞춰서 결과를 도출한다.